Força no MHS
Lista de 07 exercícios de Física com gabarito sobre o tema Força no MHS com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.
01. (URCA) Um corpo de massa 2 kg está executando um Movimento Harmônico Simples (MHS) com amplitude igual a 10 cm e período de 0,2 segundos. Suponha que as oscilações desse bloco são produzidas por uma mola de massa desprezível e a forças elástica que a mola exerce sobre o corpo obedece a Lei de Hook. Podemos afirmar que a constante de elasticidade dessa mola e o módulo da força máxima que age sobre o corpo são respectivamente, iguais a:
- 400π² (N/m) e 20π² (N)
- 200(N/m) e 20 (N)
- 200π² (N/m) e 2000π² (N)
- 20π² (N/m) e 200π² (N)
- 200π² (N/ m) e 20π² (N)
02. (UFGD) Uma oscilação harmônica é conhecida por ter força de restauração proporcional ao deslocamento. Para esse tipo de oscilação é possível dizer que:
- A frequência de oscilação independe do valor da força restauradora.
- A frequência da energia total do oscilador independe do valor da força restauradora.
- O período é o mesmo para qualquer valor da força restauradora.
- O período depende do valor da energia mecânica do sistema.
- A energia mecânica do sistema é constante.
03. (AFA) Uma partícula de massa m pode ser colocada a oscilar em quatro experimentos diferentes, como mostra a Figura 1 abaixo.
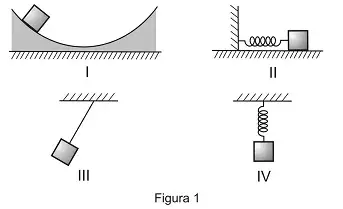
Para apenas duas dessas situações, tem-se o registro do gráfico senoidal da posição da partícula em função do tempo, apresentado na Figura 2.

Considere que não existam forças dissipativas nos quatro experimentos; que, nos experimentos II e IV , as molas sejam ideais e que as massas oscilem em trajetórias perfeitamente retilíneas; que no experimento III o fio conectado à massa seja ideal e inextensível; e que nos experimentos I e III a massa descreva uma trajetória que é um arco de circunferência.
Nessas condições, os experimentos em que a partícula oscila certamente em movimento harmônico simples são, apenas
- I e III
- II e III
- III e IV
- II e IV
04. (UEFS) O pêndulo simples é um sistema idealizado consistindo em uma partícula suspensa por um cabo leve inextensível que, quando puxado para um dos lados de sua posição de equilíbrio e liberado, oscila no plano vertical sob a influência da força gravitacional. Considere um pêndulo simples com comprimento de 9,0m e que executa 20 oscilações completas em 2,0min, em um determinado local.
Com base nessas informações, conclui-se que o módulo da aceleração da gravidade nesse local, em m/s², é, aproximadamente, igual a
- 9,53
- 9,61
- 9,87
- 9,98
- 10,05
05. (UFRR) Um bloco de massa M está preso à uma mola em uma superfície horizontal sem atrito. Inicialmente, o bloco está em repouso na posição de equilíbrio da mola (Xeq). Ele é puxado para a direita a uma distância D em relação à posição Xeq e, a partir do repouso, o bloco é liberado para oscilar. Durante as oscilações do bloco, é INCORRETO dizer que:
- Quando passa por Xeq, o bloco tem velocidade escalar máxima.
- No movimento pelo lado esquerdo de Xeq, a máxima distância que o bloco se afasta de Xeq é D.
- A velocidade do bloco nas amplitudes de oscilações é zero.
- Após uma oscilação completa, o bloco percorre 2D.
- Quando passa por Xeq, o bloco tem aceleração escalar mínima.
06. (EsPCEx) Um objeto preso por uma mola de constante elástica igual a 20 N/m executa um movimento harmônico simples em torno da posição de equilíbrio. A energia mecânica do sistema é de 0,4 J e as forças dissipativas são desprezíveis. A amplitude de oscilação do objeto é de:
- 0,1 m
- 0,2 m
- 1,2 m
- 0,6 m
- 0,3 m
07. (EsPCEx) Um ponto material oscila em torno da posição de equilíbrio O, em Movimento Harmônico Simples (MHS), conforme o desenho abaixo. A energia mecânica total do sistema é de 0,1 J, a amplitude da oscilação é de 1 m/s e o módulo da máxima velocidade é de Os extremos da trajetória desse movimento têm velocidade igual a zero (v = 0).

Desprezando as forças dissipativas a frequência da oscilação em Hertz (Hz) é
- √2/3π
- √5/π
- 5/π
- √π/3
- 1/2π