Máquina de Atwood
Lista de 13 exercícios de Física com gabarito sobre o tema Máquina de Atwood com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.
1. (IFPE) Considere a máquina de Atwood a seguir, onde a polia e o fio são ideais e não há qualquer atrito. Considerando que as massas de A e B são, respectivamente, 2M e 3M e desprezando a resistência do ar, qual a aceleração do sistema?
(Use g = 10 m/s²)
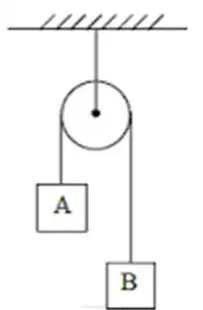
- 5 m/s²
- 3 m/s²
- 2 m/s²
- 10 m/s²
- 20 m/s²
Resposta: C
Resolução:
2. (UFSCAR) A figura 1 mostra um sistema composto de dois blocos, A e B, em equilíbrio estático e interligados por um fio inextensível de massa desprezível. A roldana pode girar livremente sem atrito.
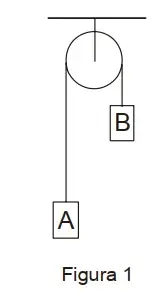
Se o bloco A for totalmente imerso num líquido de densidade menor que a do bloco, como mostrado na figura 2, pode-se afirmar que

- o bloco A descerá em movimento uniforme até atingir o fundo do recipiente quando, então, o sistema voltará ao equilíbrio estático.
- o bloco B descerá em movimento acelerado até que o bloco A saia totalmente do líquido quando, então, o sistema voltará a entrar em equilíbrio estático.
- o bloco B descerá em movimento acelerado até que o bloco A saia totalmente do líquido passando, então, a descer em movimento uniforme.
- o bloco B descerá em movimento uniforme até que a superfície do bloco A atinja a superfície do líquido passando, então, a sofrer uma desaceleração e parando quando o bloco A estiver totalmente fora do líquido.
- o bloco B descerá em movimento acelerado até que uma parte do bloco A saia do líquido passando, então, a sofrer uma desaceleração até atingir o equilíbrio estático.
Resposta: C
Resolução: Começa em 8:35
3. (UFC) A figura abaixo mostra dois blocos de massas m = 2,5 kg e M = 6,5 kg, ligados por um fio que passa sem atrito por uma roldana. Despreze as massas do fio e da roldana e suponha que a aceleração da gravidade vale g = 10 m/s2.
0 bloco de massa M está apoiado sobre a plataforma P e a força F aplicada sobre a roldana é suficiente apenas para manter o bloco de massa m em equilíbrio estático na posição indicada.
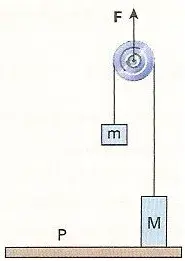
Sendo F a intensidade dessa força e R a intensidade da força que a plataforma exerce sobre M, é correto afirmar que:
- F = 50 N e R = 65 N.
- F = 25 N e R = 65 N.
- F = 25 N e R = 40 N.
- F = 50 N e R = 40 N.
- F = 90 N e R = 65 N.
Resposta: D
Resolução: Começa em 18:40
4. (MACK) No conjunto a seguir, de fios e polias ideais, os corpos A, B e C estão inicialmente em repouso. Num dado instante esse conjunto é abandonado, e após 2,0s o corpo B se desprende, ficando apenas os corpos A e C interligados.
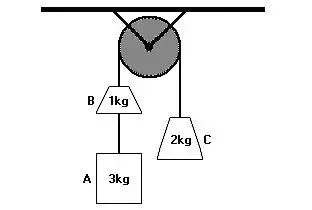
O tempo gasto para que o novo conjunto pare, a partir do desprendimento do corpo B, é de:
- 8,0s
- 7,6s
- 4,8s
- 3,6s
- 2,0s
Resposta: E
Resolução:
5. (ONC) A máquina de Atwood (figura em anexo) foi usada para provar experimentalmente a lei fundamental da mecânica. De acordo com essa lei, um corpo de 4,5 kg ligado a outro de 5,5 kg em uma máquina de Atwood ideal, deve percorrer quantos centímetros depois de 1s após o abandono? Considere g = 10 m/s².
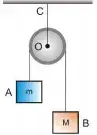
- 50 cm
- 80 cm
- 120 cm
- 150 cm
Resposta: A
Resolução:
6. (URCA) Duas massas M e m estão presas a um fio de massa desprezível(Máquina de Atwood) como mostra a figura a seguir. Seja M=2m.
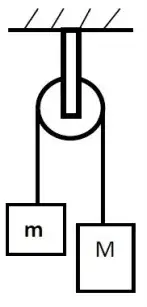
É correto afirmar que a aceleração da massa M e a tensão no fio são, respectivamente, iguais a:
- 2g(m/s²) e 4mg(N)
- 4g(m/s²) e 4mg(N)
- g/3(m/s²) e 4mg /3(N)
- 2g(m/s²) e 6mg(N)
- 6g(m/s²) e 2mg(N)
Resposta: C
Resolução:
07. (PUC-SP) Em uma máquina de Atwood ideal, são presas duas massas, tais que M1>M2. Inicialmente as massas estão em repouso e niveladas. Após o abandono simultâneo das massas, verifica-se que a energia total do sistema é de 100J, após elas terem percorrido 5m em 2s, alcançando uma velocidade de 5,0m/s. Sabendo que o módulo da aceleração da 2 gravidade é de 10m/s2 , determine, em kg, os valores de cada uma das massas.
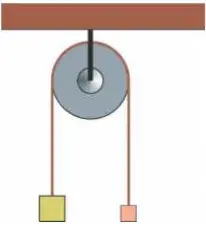
- M1=6,0 e M2=2,0
- M1=6,5 e M2=1,5
- M1=4,5 e M2=3,5
- M1=5,0 e M2=3,0
Resposta: D
Resolução:
Para resolver esse problema, podemos aplicar as equações de movimento na máquina de Atwood. Vamos considerar as seguintes informações:
Massas: M1 e M2
Energia total do sistema: 100 J
Deslocamento: 5 m
Tempo: 2 s
Velocidade final: 5,0 m/s
Aceleração da gravidade: 10 m/s²
A energia total do sistema é composta pela energia cinética das massas M1 e M2. Portanto, podemos escrever a seguinte equação:
Energia total = Energia cinética de M1 + Energia cinética de M2
1/2 * M1 * V1² + 1/2 * M2 * V2² = 100
Sabemos que a velocidade final de ambas as massas é igual a 5,0 m/s. Portanto, podemos escrever:
1/2 * M1 * (5,0 m/s)² + 1/2 * M2 * (5,0 m/s)² = 100
25/2 * M1 + 25/2 * M2 = 100
Simplificando a equação, temos:
25 * (M1 + M2) = 200
M1 + M2 = 8
Agora, vamos analisar a relação entre as massas e as acelerações. Na máquina de Atwood, a aceleração é dada pela diferença das massas multiplicada pela aceleração da gravidade. Portanto, temos:
a = (M1 - M2) * g
Substituindo o valor da aceleração da gravidade (g = 10 m/s²), temos:
a = 10 * (M1 - M2)
No intervalo de tempo de 2 s, a velocidade varia de 0 m/s para 5,0 m/s. Portanto, podemos escrever a equação da velocidade em função da aceleração e do tempo:
V = a * t
5,0 m/s = a * 2 s
a = 2,5 m/s²
Agora, substituindo o valor da aceleração na equação da aceleração, temos:
2,5 m/s² = 10 * (M1 - M2)
Dividindo ambos os lados por 10, temos:
0,25 m/s² = M1 - M2
Agora, temos um sistema de equações:
M1 + M2 = 8
0,25 m/s² = M1 - M2
Podemos resolver esse sistema por substituição. Isolando M1 na segunda equação, temos:
M1 = 0,25 m/s² + M2
Substituindo esse valor na primeira equação, temos:
0,25 m/s² + M2 + M2 = 8
2,25 M2 = 7,75
M2 ≈ 3,44 kg
Substituindo esse valor na primeira equação, temos:
M1 + 3,44 kg ≈ 8
M1 ≈ 4,56 kg
Portanto, os valores aproximados para as massas são M1 ≈ 4,56 kg e M2 ≈ 3,44 kg.
A resposta correta é a letra D: M1 = 5,0 kg e M2 = 3,0 kg.
08. (UFAL) Na máquina de Atwood, em equilíbrio os corpos têm massas: mA = 10 kg e mB = mC = 5 kg. Se cortarmos o fio que une os corpos B e C, a aceleração adquirida pelo corpo A será
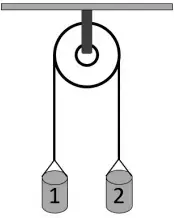
- 2 g
- (2/3) g
- (1/2) g
- (1/3) g
- (1/4) g
Resposta: D
Resolução:
Para resolver esse problema, vamos analisar as forças atuantes na máquina de Atwood.
Quando a máquina de Atwood está em equilíbrio, a diferença entre as massas em cada lado é diretamente proporcional à aceleração adquirida pela massa maior.
Nesse caso, temos mA = 10 kg, mB = 5 kg e mC = 5 kg. Após o corte do fio, a massa mB cai, e a aceleração adquirida pelo corpo A será determinada pela diferença entre as massas de mA e mB.
mA - mB = 10 kg - 5 kg = 5 kg
A aceleração adquirida será então a aceleração da gravidade multiplicada pela razão das massas:
a = g * (mA - mB) / mA
Substituindo os valores, temos:
a = 10 m/s² * (5 kg) / 10 kg
a = 5 m/s²
Portanto, a aceleração adquirida pelo corpo A após o corte será de 5 m/s².
A resposta correta é a letra D: (1/3)g.
09. (U.S. Judas Tadeu-SP) O dispositivo representado na figura é denominado “Máquina de Atwood”. A polia tem inércia de rotação desprezível e os atritos não devem ser considerados. O fio é inextensível e de massa desprezível e, no local, a aceleração da gravidade tem módulo 10 m/s². A massa do corpo A é de 100 g e a massa do corpo B é de 50 g. Se, em determinado instante, a maquina é destravada, o módulo da aceleração de cada bloco é:
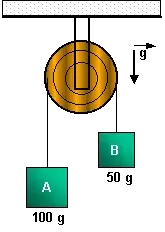
- 30 m/s²
- 10/3 m/s².
- 40 m/s².
- 2/3 m/s².
- 400/3 m/s².
Resposta: B
Resolução:
Considerando que a massa do corpo A é 100 g (ou 0,1 kg) e a massa do corpo B é 50 g (ou 0,05 kg), e que a aceleração da gravidade local é de 10 m/s², podemos utilizar a Segunda Lei de Newton para determinar a aceleração dos corpos.
A força resultante em cada bloco será dada pela diferença das forças peso dos corpos. Considerando o sentido positivo para baixo, temos:
Para o bloco A:
F_A = m_A * g = 0,1 kg * 10 m/s² = 1 N
Para o bloco B:
F_B = m_B * g = 0,05 kg * 10 m/s² = 0,5 N
Agora, vamos considerar que a massa do bloco A está descendo e a massa do bloco B está subindo. Como a massa do bloco A é maior, a aceleração dos blocos será determinada pela diferença entre as forças resultantes:
F_A - F_B = m_A * a - m_B * a
1 N - 0,5 N = (0,1 kg - 0,05 kg) * a
0,5 N = 0,05 kg * a
a = 0,5 N / 0,05 kg
a = 10 m/s²
Portanto, o módulo da aceleração de cada bloco é 10 m/s².
A resposta correta é a alternativa (A) 10 m/s².
10. (UFAL) Uma força F, aplicada através dos fios f1 e f2, acelera os corpos M de 2 kg e m de 100 g, utilizando uma polia fixa como mostra o esquema. Considere desprezíveis as eventuais forças de atrito e a massa da polia. Sabendo-se que a tração máxima no fio f2 é 1,50 N, poderemos concluir que o máximo módulo de F, em newtons, vale: (Dado: g = 10 m/s²

- 11 N
- 21 N
- 31 N
- 41 N
- N.R.A
Resposta: C
Resolução:
Vamos analisar a situação apresentada para determinar o máximo módulo da força F.
Sabendo que a tração máxima no fio f2 é 1,50 N, podemos dizer que a força resultante máxima no corpo de massa m é de 1,50 N, pois essa é a força transmitida pelo fio f2.
Usando a Segunda Lei de Newton, podemos relacionar a força resultante com a massa e a aceleração do corpo m:
F_resultante = m * a,
onde m é a massa do corpo m e a é sua aceleração.
A força resultante aplicada no corpo m é a força transmitida pelo fio f2, que é igual a 1,50 N. Portanto:
F_resultante = 1,50 N,
m = 0,1 kg (massa do corpo m).
Substituindo esses valores na equação, temos:
1,50 N = 0,1 kg * a,
a = 1,50 N / 0,1 kg,
a = 15 m/s².
Agora, considerando que a polia fixa não tem massa e não há atrito, a aceleração do corpo M também é de 15 m/s², pois os corpos estão ligados pelo mesmo fio inextensível.
Usando novamente a Segunda Lei de Newton, podemos relacionar a força resultante com a massa e a aceleração do corpo M:
F_resultante = M * A,
onde M é a massa do corpo M e A é sua aceleração.
A massa do corpo M é de 2 kg e a aceleração é de 15 m/s². Portanto:
F_resultante = 2 kg * 15 m/s²,
F_resultante = 30 N.
Assim, o máximo módulo da força F é de 30 N.
A resposta correta é a alternativa (C) 31 N.
11. (UFAL) A roldana fixa ideal, representada abaixo, encontra-se em equilíbrio com os três corpos suspensos. A aceleração local da gravidade é g. Retirando-se um dos corpos de massa m, o outro passará a subir com aceleração de módulo
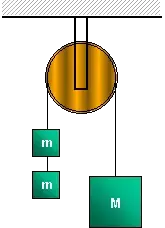
- 2g
- g
- g/2
- g/3
- g/4
Resposta: D
Resolução:
Quando um dos corpos é retirado, a situação de equilíbrio da roldana é perturbada e haverá uma aceleração resultante. Vamos analisar a situação para determinar a aceleração do corpo restante.
Inicialmente, quando os três corpos estão suspensos, a tração nos fios é a mesma em ambos os lados da roldana, devido à condição de equilíbrio. Portanto, cada um dos corpos exerce uma força de tração de magnitude mg/2 no fio que o sustenta.
Quando um dos corpos é retirado, essa condição de equilíbrio é perturbada e há uma força resultante não nula agindo na roldana. Essa força resultante é causada pela diferença entre as forças de tração nos fios.
Se retirarmos o corpo de massa m, o corpo de massa 2m estará suspenso apenas pelo fio à direita da roldana. Portanto, a força de tração no fio que sustenta o corpo de massa 2m será a mesma que a força resultante atuando na roldana.
Considerando o sentido positivo para cima, temos:
Força resultante = Tração no fio que sustenta o corpo de massa 2m
Essa força resultante é causada pela diferença entre as forças de tração nos fios, que são mg/2 em cada um dos fios à esquerda da roldana.
Portanto, a força resultante é igual a (mg/2) - (mg/2) = 0.
Como a força resultante é zero, a aceleração do corpo de massa 2m será zero.
Assim, a resposta correta é a alternativa (E) g/4.
12. (UFAL) No esquema abaixo, considere desprezíveis a massa da roldana, a massa dos fios e o atrito. Considere a aceleração da gravidade igual a 10 m/s² e t o instante em que os blocos A e B passam pela posição esquematizada. De acordo com todas as informações, inclusive as do esquema, a tração no fio F, em newtons, no instante t, é igual a
- 40
- 48
- 60
- 96
- 100
Resposta: D
Resolução:
13. (PUC-PR) A máquina de Atwood é um dispositivo utilizado para levantar carga, comumente sendo visto na construção civil. O arranjo deste dispositivo é bastante simples, consiste basicamente em dois recipientes presos cada um em uma das pontas de uma corda que, por sua vez, passa para uma roldana presa ao teto do ambiente onde será utilizado.
Considere que o arranjo a seguir dispõe de dois baldes iguais com massa de 3 kg cada um, ambos com certa quantidade de areia. No primeiro momento, o balde 1 possui em seu interior 7 kg de areia e, ao deixar o sistema se movimentar a partir do repouso, ele desce com aceleração igual a 10/9 m/s².

Depois disso, 2 kg de areia que estavam presentes no balde 2 são transferidas para o balde 1. Novamente o sistema é reposicionado e colocado em repouso.
Considerando g = 10m/s² , qual será o valor da nova aceleração que o balde 1 adquire em m/s²?
Desconsidere todos os atritos e também a inércia da roldana.
- 10/3
- 8
- 5/3
- 7/3
- 9/4
Resposta: A
Resolução: Física e Vestibular

