Movimento Harmônico Simples
Lista de 10 exercícios de Física com gabarito sobre o tema Movimento Harmônico Simples com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.
1. (FATEC-SP) Para uma partícula em movimento harmônico simples:
- a trajetória é uma senóide.
- a trajetória é uma circunferência e a velocidade do ponto é constante em intensidade.
- a aceleração tem módulo diretamente proporcional ao da elongação, em cada instante.
- a aceleração é constante.
- as afirmações anteriores são falsas.
Resposta: C
Resolução: No MHS, a aceleração é diretamente proporcional e oposta à elongação (deslocamento) da partícula em relação à sua posição de equilíbrio. Isso significa que quanto maior for a elongação, maior será a aceleração, e a direção da aceleração é sempre oposta à elongação. Portanto, a aceleração não é constante, mas varia ao longo da trajetória da partícula, e sua relação com a elongação é direta.
2 (U.E.MARINGÁ-PR) Uma partícula realiza movimento harmônico simples em relação a um dado referencial. Nessa condição, podemos afirmar que:
- sua energia potencial é inversamente proporcional à abscissa que define sua posição.
- sua velocidade ênula quando a abscissa x é nula.
- sua aceleração varia linearmente com o tempo.
- sua velocidade é nula quando sua aceleração tem módulo máximo.
- sua velocidade máxima independe da amplitude do movimento.
Resposta: D
Resolução:
A resposta correta é (D), sua velocidade é nula quando sua aceleração tem módulo máximo.
A energia potencial de uma partícula em movimento harmônico simples é dada por:
U = kx²/2
Onde:
k é a constante elástica
x é a elongação da partícula
Portanto, a energia potencial é diretamente proporcional à elongação da partícula.
A velocidade de uma partícula em movimento harmônico simples é dada por:
v = x'(t)
Onde:
v é a velocidade da partícula
x'(t) é a derivada da elongação da partícula em relação ao tempo
Portanto, a velocidade da partícula é nula quando a elongação da partícula é nula.
A aceleração de uma partícula em movimento harmônico simples é dada por:
a = -kx/m
Onde:
a é a aceleração da partícula
k é a constante elástica
m é a massa da partícula
Portanto, a aceleração da partícula varia linearmente com a elongação da partícula, mas não com o tempo.
A velocidade máxima de uma partícula em movimento harmônico simples é dada por:
v_m = √kx/m
Onde:
v_m é a velocidade máxima da partícula
k é a constante elástica
m é a massa da partícula
Portanto, a velocidade máxima da partícula depende da amplitude do movimento.
Portanto, a resposta correta é (D), sua velocidade é nula quando sua aceleração tem módulo máximo.
Aqui está uma explicação mais detalhada de cada afirmação:
Afirmação (A)
A energia potencial de uma partícula em movimento harmônico simples é dada por:
U = kx²/2
Onde:
k é a constante elástica
x é a elongação da partícula
Portanto, a energia potencial é diretamente proporcional à elongação da partícula. Isso significa que, quando a elongação da partícula é nula, a energia potencial da partícula é zero.
Afirmação (B)
A velocidade de uma partícula em movimento harmônico simples é dada por:
v = x'(t)
Onde:
v é a velocidade da partícula
x'(t) é a derivada da elongação da partícula em relação ao tempo
Portanto, a velocidade da partícula é nula quando a elongação da partícula é nula.
Afirmação (C)
A aceleração de uma partícula em movimento harmônico simples é dada por:
a = -kx/m
Onde:
a é a aceleração da partícula
k é a constante elástica
m é a massa da partícula
Portanto, a aceleração da partícula varia linearmente com a elongação da partícula, mas não com o tempo.
Afirmação (E)
A velocidade máxima de uma partícula em movimento harmônico simples é dada por:
v_m = √kx/m
Onde:
v_m é a velocidade máxima da partícula
k é a constante elástica
m é a massa da partícula
Portanto, a velocidade máxima da partícula depende da amplitude do movimento.
3. (EPUSP) Um ponto material executa movimento harmônico simples. Sua energia cinética é máxima:
- nos pontos de abscissa máxima.
- nos pontos de aceleração máxima.
- nos pontos onde a aceleração é nula.
- em ponto nenhum: a energia cinética é constante pelo princípio da conservação da energia.
- Nenhuma das anteriores.
Resposta: C
Resolução:
A resposta correta é (C), nos pontos onde a aceleração é nula.
No movimento harmônico simples, a energia mecânica total é constante. Essa energia é composta pela energia cinética e pela energia potencial. A energia cinética é máxima quando a velocidade é máxima, que ocorre nos pontos onde a aceleração é nula.
Portanto, a resposta correta é (C).
Explicação:
A energia mecânica total de um sistema é dada por:
E = K + U
Onde:
K é a energia cinética;
U é a energia potencial.
No movimento harmônico simples, a energia mecânica total é constante:
E = constante
A energia cinética é dada por:
K = 1/2mv²
Onde:
m é a massa do corpo;
v é a velocidade do corpo.
A energia potencial elástica é dada por:
U = 1/2kx²
Onde:
k é a constante elástica da mola;
x é a distância entre a posição atual do corpo e a posição de equilíbrio.
A velocidade é máxima quando a aceleração é nula. No movimento harmônico simples, a aceleração é dada por:
a = -kx/m
Onde:
a é a aceleração do corpo;
k é a constante elástica da mola;
m é a massa do corpo;
x é a distância entre a posição atual do corpo e a posição de equilíbrio.
Portanto, a energia cinética é máxima nos pontos onde a aceleração é nula.
04. (Fuvest) Um trapezista abre as mãos, e larga a barra de um trapézio, ao passar pelo ponto mais baixo da oscilação. Desprezando-se o atrito, podemos afirmar que o trapézio:
- para de oscilar.
- aumenta a amplitude de oscilação.
- tem seu período de oscilação aumentado.
- não sofre alteração na sua freqüência
- aumenta sua energia mecânica.
Resposta: D
Resolução: Se o trapézio puder ser entendido como um pêndulo simples cujo período é
o período não depende da massa, não se altera, assim como a frequência que é o seu inverso. (Fonte: pir2.forumeiros.com)
05. (Unitau-SP) Um corpo de massa m, ligado a uma mola de constante elástica k, está animado de um movimento harmônico simples. Nos pontos em que ocorre a inversão no sentido do movimento:
- são nulas a velocidade e a aceleração
- são nulas a velocidade e a energia potencial
- o módulo da aceleração e a energia potencial são máximas
- a energia cinética é máxima e a energia potencial é mínima
- a velocidade, em módulo, e a energia potencial são máximas
Resposta: C
Resolução:
06. (UDESC) Uma das extremidades de uma corda está presa a um suporte fixo no topo de um poço vertical de uma mina com profundidade igual a 161,0 m. A corda fica esticada pela ação do peso de uma caixa de minérios com massa igual a 25,0 kg, presa na extremidade inferior da corda, que está 1,0 m acima da parte inferior da mina. A massa da corda é igual a 4,0 kg. Um mineiro, no fundo da mina, balançando horizontalmente a extremidade inferior da corda, envia um sinal para seu colega que está no topo da mina. Sabendo-se que um ponto da corda realiza um movimento harmônico simples (MHS) com freqüência de 4,0 Hz, e desconsiderando-se o peso da corda, a velocidade da onda transversal que se propaga na corda e o comprimento de onda são, respectivamente:
- 160,0 m/s e 40,0 m.
- 80,0 m/s e 20,0 m.
- 100,0 m/s e 400,0 m.
- 100,0 m/s e 25,0 m.
- 4,0 m/s e 100,0 m.
Resposta: D
Resolução:
A resposta correta é a (4).
A velocidade de uma onda transversal em uma corda é dada pela fórmula:
v = √(T / μ)
Onde:
v é a velocidade da onda
T é a tensão na corda
μ é a massa linear da corda
A tensão na corda é dada pela fórmula:
T = mg
Onde:
T é a tensão na corda
m é a massa da caixa de minérios
g é a aceleração da gravidade
Assim, a tensão na corda é:
T = 25,0 kg * 9,8 m/s² = 245 N
A massa linear da corda é dada pela fórmula:
μ = m / L
Onde:
μ é a massa linear da corda
m é a massa da corda
L é o comprimento da corda
Assim, a massa linear da corda é:
μ = 4,0 kg / (161,0 m - 1,0 m) = 0,0024 kg/m
Portanto, a velocidade da onda transversal na corda é:
v = √(245 N / 0,0024 kg/m) = 100,0 m/s
O comprimento de onda é dado pela fórmula:
λ = v / f
Onde:
λ é o comprimento de onda
v é a velocidade da onda
f é a frequência da onda
Assim, o comprimento de onda é:
λ = 100,0 m/s / 4,0 Hz = 25,0 m
Portanto, a resposta correta é a (4). A velocidade da onda transversal na corda é de 100,0 m/s e o comprimento de onda é de 25,0 m.
As outras respostas estão incorretas por:
(A) A velocidade da onda transversal é de 100,0 m/s, não 160,0 m/s.
(B) O comprimento de onda é de 25,0 m, não 40,0 m.
(C) A velocidade da onda transversal é de 100,0 m/s, não 400,0 m/s.
(E) A velocidade da onda transversal é de 4,0 m/s, não 100,0 m/s.
07. (Fatec) O período de oscilação de um pêndulo simples pode ser calculado por T=2 ™Ë(L/g), onde L é o comprimento do pêndulo e g a aceleração da gravidade (ou campo gravitacional) do local onde o pêndulo se encontra.
Um relógio de pêndulo marca, na Terra, a hora exata.
É correto afirmar que, se este relógio for levado para a Lua,
- atrasará, pois o campo gravitacional lunar é diferente do terrestre.
- não haverá alteração no período de seu pêndulo, pois o tempo na Lua passa da mesma maneira que na Terra.
- seu comportamento é imprevisível, sem o conhecimento de sua massa.
- adiantará, pois o campo gravitacional lunar é diferente do terrestre.
- não haverá alteração no seu período, pois o campo gravitacional lunar é igual ao campo gravitacional terrestre.
Resposta: A
Resolução:
O período de oscilação de um pêndulo simples é inversamente proporcional à aceleração da gravidade. Na Lua, a aceleração da gravidade é cerca de seis vezes menor do que na Terra. Portanto, o período de oscilação do pêndulo na Lua será cerca de seis vezes maior.
Assim, o relógio de pêndulo atrasará na Lua.
As outras respostas estão incorretas por:
(B) O período de oscilação do pêndulo depende da aceleração da gravidade, que é diferente na Lua e na Terra.
(C) O comportamento do relógio de pêndulo é previsível, pois o período de oscilação é calculado com base na aceleração da gravidade.
(D) O relógio de pêndulo atrasará, pois a aceleração da gravidade na Lua é menor do que na Terra.
(E) O campo gravitacional lunar é diferente do campo gravitacional terrestre.
08. (EsPCEx)Peneiras vibratórias são utilizadas na indústria de construção para classificação e separação de agregados em diferentes tamanhos. O equipamento é constituído de um motor que faz vibrar uma peneira retangular, disposta no plano horizontal, para separação dos grãos. Em uma certa indústria de mineração, ajusta-se a posição da peneira de modo que ela execute um movimento harmônico simples (MHS) de função horária x 8 cos (8 π t), onde x é a posição medida em centímetros e t, o tempo em segundos.
O número de oscilações a cada segundo executado por esta peneira é de
- 2
- 4
- 8
- 16
- 32
Resposta: B
Resolução:
09. (Uel) Um movimento harmônico simples é descrito pela função x=0,050 cos(2πt+π), em unidades do Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades do Sistema Internacional, valem, respectivamente,
- 0,050 e 1,0
- 0,050 e 0,50
- π e 2π
- 2π e π
- 2,0 e 1,0
Resposta: A
Resolução:
A amplitude de um movimento harmônico simples é o valor máximo da posição do corpo em relação à sua posição de equilíbrio. No caso da função dada, a amplitude é igual ao módulo do coeficiente da função senoidal, que é 0,050 m.
O período de um movimento harmônico simples é o intervalo de tempo necessário para que o corpo complete uma oscilação completa. No caso da função dada, o período é dado pelo intervalo de tempo entre dois máximos consecutivos da função, que é 2π / 2π = 1 s.
Assim, a amplitude e o período são, respectivamente, 0,050 m e 1 s.
As outras respostas estão incorretas por:
(B) A amplitude é 0,050 m, não 0,50 m.
(C) A amplitude é 0,050 m, não π.
(D) O período é 1 s, não 2π.
(E) O período é 1 s, não 2.
Aqui está a explicação detalhada:
A amplitude de um movimento harmônico simples é dada pela fórmula:
A = |A|
Onde:
A é a amplitude
|A| é o módulo do coeficiente da função senoidal
No caso da função dada, a amplitude é:
A = |0,050| = 0,050 m
O período de um movimento harmônico simples é dado pela fórmula:
T = 2π / ω
Onde:
T é o período
ω é a frequência angular
A frequência angular é dada pela fórmula:
ω = 2π / T
Portanto, o período é:
T = 2π / ω = 2π / (2π / 1) = 2π * 1 / 2π = 1 s
10. (Fuvest) O gráfico representa, num dado instante, a velocidade transversal dos pontos de uma corda, na qual se propaga uma onda senoidal na direção do eixo dos x.
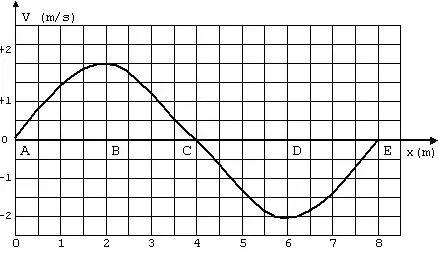
A velocidade de propagação da onda na corda é de 24m/s. Sejam A, B, C, D e E pontos da corda. Considere, para o instante representado, as seguintes afirmações:
I. A frequência da onda é 0,25Hz.
II. Os pontos A, C e E têm máxima aceleração transversal (em módulo).
III. Os pontos A, C e E têm máximo deslocamento transversal (em módulo).
IV. Todos os pontos da corda se deslocam com velocidade de 24m/s na direção do eixo x
São corretas as afirmações
- todas.
- somente IV.
- somente II e III.
- somente I e II.
- somente II , III e IV
Resposta: B
Resolução: