Unioeste 2022: Matemática

43. (Unioeste) Suponha que f: R → R é uma função afim dada pela expressão f(x) = αx + b com α e b constantes reais. Então podemos afirmar que:

1. a) se x1, x2, x3, ..., xn forma uma progressão aritmética, então f(x1), f(x2), f(x3), ..., f(xn) também forma uma progressão aritmética.
2. se x1, x2, x3, ..., xn forma uma progressão aritmética, então f(x1), f(x2), f(x3), ..., f(xn) forma uma progressão geométrica.
3. se x1, x2, x3, ..., xn forma uma progressão geométrica, então f(x1), f(x2), f(x3), ..., f(xn) forma uma progressão aritmética.
4. se x1, x2, x3, ..., xn forma uma progressão geométrica, então f(x1), f(x2), f(x3), ..., f(xn) também forma uma progressão geométrica.
5. se x1, x2, x3, ..., xn forma uma progressão aritmética, então f(x1), f(x2), f(x3), ..., f(xn) não forma progressão aritmética e nem progressão geométrica.

44. (Unioeste) Considere f, g: R → R duas funções determinadas pelas expressões f(x) = sen(cos x) e 𝑔(x) = cos(sen x). A respeito das funções f e 𝑔 é CORRETO afirmar que:

1. são ambas invertíveis e uma é a inversa da outra.
2. possuem o mesmo conjunto imagem.
3. f(x) = 𝑔(x) para todo x ∈ R.
4. são ambas periódicas de período π.
5. satisfazem f(x) = f(-x) e 𝑔(x) = 𝑔(-x) para todo real.

45. (Unioeste) Um tanque de óleo possui formato de cilindro circular reto e está posicionado deitado em relação ao solo, isto é, os planos que contém as faces circulares é perpendicular ao plano do solo. O tanque contém óleo de forma que a qualquer secção do cilindro, paralela às faces circulares, mostra a altura do óleo em relação ao solo, de 1,5m, conforme a figura abaixo.

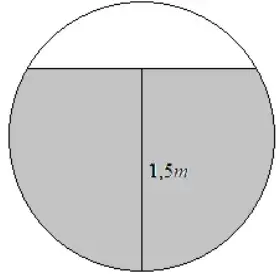
O comprimento do tanque é de h metros e o raio das faces circulares é de 1 metro. Desprezando a espessura do material com o qual o tanque é fabricado, qual o volume do óleo contido no tanque?

1. h/12 (8π + 3)
2. h/12 (4π + √3)
3. h/4 (3π + 1)
4. h/12 (8π + 3 √3)
5. h/12 (4π + 3 √3)

46. (Unioeste) A soma dos valores possíveis da constante α ∈ R que satisfazem a equação matricial

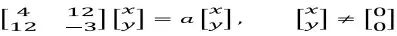é igual a:

1. -156
2. -1
3. 1
4. 25
5. 156

47. (Unioeste) A única unidade básica de saúde de um bairro que aplica vacinas contra uma determinada doença possui 3 equipes de vacinação: A, B e C.

Por conta da diferença de experiência de cada equipe em relação a esta vacinação, a equipe A consegue vacinar uma pessoa a cada 5 minutos, a equipe B vacina uma pessoa a cada 4 minutos e a equipe C vacina uma pessoa a cada 3 minutos.

Considerando que as 3 equipes trabalham 8 horas por dia e que a população do bairro é de 5.000 pessoas, o número mínimo de dias que a unidade de saúde precisa para vacinar toda a população do bairro é:

1. 11
2. 12
3. 13
4. 14
5. 15

48. (Unioeste) Determinada empresa vende x unidades de um produto por p1(x) = 50x. Sabe-se que o custo com material para produzir x unidades é p2(x) = 11x + 5000. Além disso, o custo com mão de obra para a produção de x unidades é p3(x) = 5x. Os valores p1(x), p2(x) e p3(x) são expressos em Reais.

Os produtos são entregues nas residências dos clientes a um custo para a empresa de R$ 6,00 por unidade. Se q é o polinômio que representa o lucro na venda de x unidades, então

1. q(x) = 40x – 5000.
2. q(x) = 34x + 5000.
3. q(x) = 28x – 5000.
4. q(x) = 28x + 5000.
5. q(x) = 34x – 5000.

49. (Unioeste) Considere uma circunferência de raio 1 e centro no ponto (4,2). Denote por (4, y0) e (4, y1), com y0 < y1 os dois pontos da circunferência cuja abscissa é 4.

Seja r a reta que tem inclinação 3/5 e passa pelo ponto (4, y0). Seja a reta que intercepta a reta r no ponto de abscissao -1 passa pelo ponto (0, -1).

Se a reta s intercepta a circunferência em dois pontos, então é correto afirmar que as coordenadas desses dois pontos são

1. (4,3) e (3,2)
2. (4,3) e (5,2)
3. (4,1) e (5,2)
4. (7/2, - √3/2 + 2) e (9/2, √3/2 + 2)
5. (7/2, √3/2 + 2) e (9/2, - √3/2 + 2)