Santa Casa 2022:
(Santa Casa 2022) O gráfico mostra a distribuição da população mundial sob diversos tipos de regimes políticos, de 1816 até 2015.
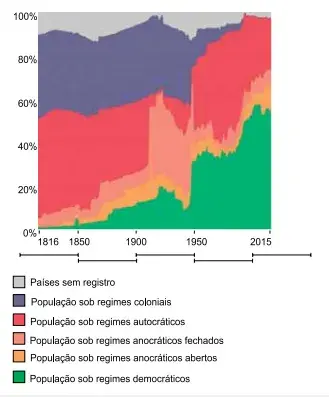
De acordo com o gráfico, pode-se afirmar que
- dois terços da população mundial esteve sob regime autocrático em algum ano do intervalo analisado.
- no início do século XXI já não havia população sob regime político colonial nos países com registro.
- cerca de dois terços da população mundial vivia sob regimes democráticos em 2015.
- cerca de 40% da população mundial estava sob regime anocrático no início do século XX.
- por volta de 1950 mais de 60% da população mundial estava sob regime anocrático fechado.
(Santa Casa 2022) A figura indica as medidas internas do diâmetro da base e da altura de um pote, de forma aproximadamente cilíndrica, que está cheio de arroz.

Admitindo-se que a densidade do arroz seja de 1,2 g/cm³ e que a massa de um grão de arroz seja de 0,04 g, o número aproximado de grãos de arroz contidos nesse pode está entre
- 60 e 90 mil.
- 200 e 300 mil.
- 20 e 50 mil.
- 120 e 170 mil.
- 5 e 10 mil.
(Santa Casa 2022) O projeto de um lago prevê uma forma composta por cinco figuras planas: dois semicírculos, dois triângulos retângulos isósceles e um retângulo. As medidas envolvidas no projeto estão descritas na figura a seguir.

A área total ocupada pelo lago, em m², é igual a
- 9300√2 + 1600π
- 13200 + 1600π
- 9300√2 + 1700π
- 13200 + 2200π
- 13200 + 1700π
(Santa Casa 2022) A figura indica o projeto de construção de uma arena de esportes, sendo AB a representação de uma luminária cujo ponto mais próximo do chão está a 5,5 m.
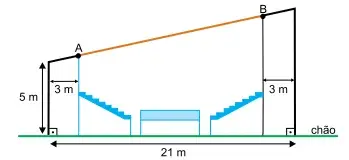
O comprimento de AB, em metros, é igual a
- 3√37
- 2√37
- 2,5√37
- 21,5 - 2√37
- 21,5 - √37
(Santa Casa 2022) Marca-se com caneta a letra A em um baralho de 52 cartas, conforme indicam as figuras.

Na posição em que está o baralho, as 52 cartas são embaralhadas aleatoriamente, de forma que as marcas de caneta nas cartas fiquem sempre na mesma face do bloco do baralho. Nesse embaralhamento, a probabilidade de que a face marcada com caneta passe a indicar novamente uma letra A é igual a
- 22!22!4!4! / 52!
- 44!8! / 52!
- 44!8!4! / 52!
- 44!4! / 52!
- 44!4!4! / 52!
(Santa Casa 2022) O programa de sócio torcedor de uma agremiação esportiva cobra mensalidade de R$ 50,00 dos sócios. Atualmente, o programa conta com 600 sócios e a agremiação estima que a cada R$ 5,00 de aumento na mensalidade irá perder 8 sócios. Considerando apenas aumentos mensais de R$ 5,00, o maior faturamento mensal que esse programa de sócio torcedor pode gerar para a agremiação é de
- R$ 72.240,00.
- R$ 78.250,00.
- R$ 80.420,00.
- R$ 82.280,00.
- R$ 86.420,00.
(Santa Casa 2022) De acordo com a lei de Newton sobre processo de resfriamento, a temperatura T(t) de uma substância é atingida em t minutos segundo o modelo dado por T(t) = (T0 – TR)e–rt + TR, em que T0 é a temperatura inicial da substância, TR é a temperatura do ambiente e r é a constante de resfriamento da substância, com todas as temperaturas dadas em uma mesma unidade de medida.
Laís vai resfriar um alimento que está à temperatura de 100 ºC na sua cozinha que, por sua vez, está à temperatura de 20 ºC. Usando In 0,225 = –1,49 nos cálculos, se a taxa de resfriamento do alimento é igual a 0,05, o tempo que Laís deve levar para resfriá-lo até a temperatura de 38 ºC, em minutos, será igual a
- 27,6.
- 28,4.
- 29,8.
- 26,4.
- 25,5.
(Santa Casa 2022) Duas progressões aritméticas, de n termos cada, possuem soma dos termos dadas por 1 + 3 + 5 + 7 + ⋅⋅⋅ + x e 2 + 4 + 6 + ⋅⋅⋅ + (x + 1), sendo x um número natural ímpar.
Sabendo-se que
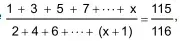 o valor de x que resolve tal equação é
o valor de x que resolve tal equação é
- 113.
- 115.
- 59.
- 229.
- 197.
(Santa Casa 2022) Em relação ao quadrilátero ABCD indicado a seguir, sabe-se que CB = 0,5, CD = 0,3, AD = cos a e os ângulos ABD e BDC são retos.
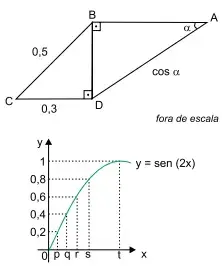
Usando informações do gráfico da função definida por y = sen (2x), de IR em IR, é correto dizer que a medida de α, em radianos, é igual a
- q.
- t.
- p.
- r.
- s
(Santa Casa 2022) Considere as funções
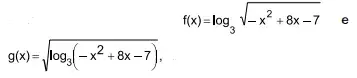 delimitadas a valores reais de x
tal que 2 ≤ x ≤ 6. A diferença entre os valores máximos de g(x) e f(x), nessa ordem, é igual a
delimitadas a valores reais de x
tal que 2 ≤ x ≤ 6. A diferença entre os valores máximos de g(x) e f(x), nessa ordem, é igual a
- 9/41
- √2 -1
- √3 -1
- 1/3
- 1/9