Unicamp 2021-1: Matemática

1. (Unicamp 2021) O número de anagramas da palavra REFLORESTAMENTO que começam com a sequência FLORES é

1. 9!.
2. 9!/2!.
3. 9!/(2! 2!).
4. 9!/(2! 2! 2!).

2. (Unicamp 2021) A soma dos valores de 𝑥 que resolvem a equação

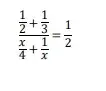
é igual a

1. 14/3.
2. 16/3.
3. 18/3.
4. 20/3.

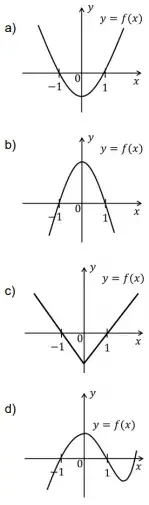
3. (Unicamp 2021) Sejam p(x) e q(x) polinômios de grau 2 tais que p(0) < q(0). Sabendo que p(1) = q(1) e p(–1) = q(–1), o gráfico de f(𝑥) = p(x) – q(x) pode ser representado por

O texto abaixo será utilizado nas questões 24 e 25.

O projeto PRODES – Monitoramento do desmatamento das formações florestais na Amazônia Legal -, do INPE (Instituto Nacional de Pesquisas Espaciais), monitora as áreas desmatadas da Amazônia legal e mantém um registro da área desmatada por ano. Um levantamento sobre esses dados a partir de 2016 mostrou que em 2019 houve um acréscimo de 35% da área desmatada em relação a 2018, de 45% em relação a 2017 e de 28% em relação a 2016.

(Fonte: http://terrabrasilis.dpi.inpe.br. Acessado em 12/12/2020.)

4. (Unicamp 2021) Sabendo que a soma das áreas desmatadas nos anos de 2017, 2018 e 2019 foi de 24.600 km², a área desmatada no ano de 2019 está entre

1. 8.601 km² e 9.200 km².
2. 9.201 km² e 9.800 km².
3. 8.801 km² e 10.400 km².
4. 10.401 km² e 11.200 km².

O texto abaixo será utilizado nas questões 24 e 25.

O projeto PRODES – Monitoramento do desmatamento das formações florestais na Amazônia Legal -, do INPE (Instituto Nacional de Pesquisas Espaciais), monitora as áreas desmatadas da Amazônia legal e mantém um registro da área desmatada por ano. Um levantamento sobre esses dados a partir de 2016 mostrou que em 2019 houve um acréscimo de 35% da área desmatada em relação a 2018, de 45% em relação a 2017 e de 28% em relação a 2016.

(Fonte: http://terrabrasilis.dpi.inpe.br. Acessado em 12/12/2020.)

5. (Unicamp 2021) Considerando os dados apresentados, relativos ao período analisado, é correto afirmar:

1. O ano que teve a menor área desmatada foi 2016.
2. A área desmatada em 2019 corresponde a 80% da área total desmatada no período de 2017 a 2018.
3. A área desmatada em 2018 foi 35% menor do que em 2019.
4. A área desmatada em 2018 foi menor que a área desmatada em 2016.

6. (UNICAMP 2021) Se 𝑓(𝑥) = log10(𝑥) e 𝑥 > 0, então 𝑓(1/𝑥) + 𝑓(100𝑥) é igual a

1. 1.
2. 2.
3. 3.
4. 4.

7. (Unicamp 2021) Considere que os ângulos internos de um triângulo formam uma progressão aritmética. Dado que a, b, c são as medidas dos lados do triângulo, sendo a < b < c, é correto afirmar que

1. b² + ac = a² + c².
2. a² + bc = b² + c².
3. a² – bc = b² + c².
4. b² – ac = a² + c².

8. (Unicamp 2021) A figura abaixo exibe um quadrado ABCD em que M é o ponto médio do lado CD.

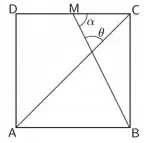
Com base na figura, tg(θ) + tg(α) é igual a

1. 7.
2. 6.
3. 5.
4. 4.

9. (Unicamp 2021) Considere 𝑎, 𝑏, 𝑐, 𝑑 termos consecutivos de uma progressão aritmética de números reais com razão r ≠ 0.

Denote por 𝐷 o determinante da matriz $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$

É correto afirmar que $\frac{𝐷}{\mathrm{r²}}$ vale

1. -1
2. -2
3. -3
4. -4

10. (Unicamp 2021) Seja x um número real tal que os primeiros três termos de uma progressão geométrica infinita são 1, 2x, –3x + 1, nesta ordem. Sabendo que todos os termos da progressão são positivos, a soma de todos eles é igual a

1. 3/2.
2. 2.
3. 5/2.
4. 3.

11. (Unicamp 2021) No plano cartesiano, considere a reta de equação x + 2y = 4, sendo A, B os pontos de interseção dessa reta com os eixos coordenados. A equação da reta mediatriz do segmento de reta AB é dada por

1. 2x – y = 3.
2. 2x – y = 5.
3. 2x + y = 3.
4. 2x y = 5.

12. (Unicamp 2021) No início do expediente do dia 16 de março de 2020, uma farmácia colocou à disposição dos clientes um frasco cilíndrico de 500 ml (500 cm³) de álcool em gel para higienização das mãos. No final do expediente, a coluna de álcool havia baixado 5 cm.

Sabendo que a base do cilindro tem diâmetro de 6 cm e admitindo o mesmo consumo de álcool em gel nos dias seguintes, calcula-se que o frasco ficou vazio no dia

1. 17 de março.
2. 18 de março.
3. 19 de março.
4. 20 de março.