Função Horária ou do Tempo no MHS

01. (Fuvest) Os smartphones modernos vêm equipados com um acelerômetro, dispositivo que mede acelerações a que o aparelho está submetido.

O gráfico foi gerado a partir de dados extraídos por um aplicativo do acelerômetro de um smartphone pendurado por um fio e colocado para oscilar sob a ação da gravidade. O gráfico mostra os dados de uma das componentes da aceleração (corrigidos por um valor de referência constante) em função do tempo.

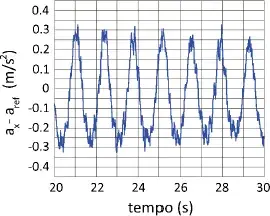
Com base nos dados do gráfico e considerando que o movimento do smartphone seja o de um pêndulo simples a ângulos pequenos, o comprimento do fio é de aproximadamente:

Note e adote:

Use π = 3.

Aceleração da gravidade: g = 10 m/s².

1. 5 cm
2. 10 cm
3. 50 cm
4. 100 cm
5. 150 cm

02. (EsPCEx) Um ponto material realiza um movimento harmônico simples (MHS) sobre um eixo 0x, sendo a função horária dada por:

x = 0,08 . cos (π/4 t + π), para x em metros e t em segundos

A pulsação, a fase inicial e o período do movimento são, respectivamente,

1. π/4 rad/s, 2 π rad, 6 s.
2. 2π rad, π/4 rad/s , 8 s.
3. π/4 rad/s, π rad, 4 s.
4. π rad/s, 2 π rad, 6 s.
5. π/4 rad/s, π rad, 8 s.

03. (UFU) O gráfico a seguir representa o movimento oscilatório de um objeto preso a uma mola.

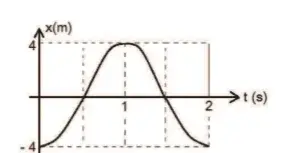
Qual das alternativas indica corretamente a função horária desse movimento harmônico?

1. x = 4 cos (2π t + π).
2. x = - 4 sen (π t + π).
3. x = 4 cos (π t + 2π).
4. x = 4 cos (π t + π).

04. (UPE) Um gerador que produz energia a partir das ondas do mar consiste essencialmente em uma boia que sobe e desce com o movimento das ondas, fazendo um motor girar e produzir eletricidade. Com o objetivo de verificar a disponibilidade e eficiência dessa forma de geração de energia na costa pernambucana. um grupo de pesquisadores instalou uma boia no mar. Um trecho do gráfico da altura da boia y em função do tempo t é mostrado a seguir

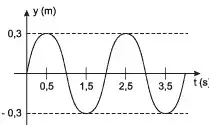
A altura foi medida em relação ao nível da água do mar sem ondas. Com base nessas:

1. y(t) = (0,3 m) sen(πt)
2. y(t) = (0,3 m) cos(πt)
3. y(t) = (0,3 m) sen(0,5πt)
4. y(t) = (30 m) sen(1,5πt)
5. y(t) = (30 m) cos(1,5πt)

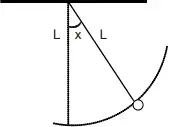
05. (PUC-RS) Ao visitar o Panteon, em Paris, Tales conheceu o Pêndulo de Foucault. O esquema abaixo indica a posição do pêndulo fixado a uma haste horizontal, num certo instante.

Sendo L o seu comprimento e x o ângulo em relação a sua posição de equilíbrio, então a altura h do pêndulo em relação à haste horizontal é expressa pela função

1. h(x) = L cos (x)
2. h(x) = L sen (x)
3. h(x) = L sen (2x)
4. h(x) = L cos (2x)
5. h(x) = 2L cos (x)

06. (EN) Analise o gráfico abaixo.

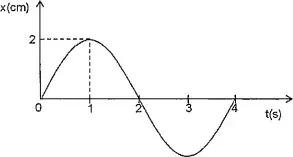
O gráfico acima representa a posição x de uma partícula que realiza um MHS (Movimento Harmônico Simples), em função do tempo t.

A equação que relaciona a velocidade v, em cm/s, da partícula com a sua posição x é

1. v² = π² (1 - x²)
2. v² = π²/2 (1 - x²/2)
3. v² = π² (1 + x²)
4. v² = π² (1 - x²/4)
5. v² = π²/4 (1 - x²)

07. (UFV-MG) Duas partículas descrevem movimentos harmônicos simples representados nos gráficos (I) e (II) a seguir.

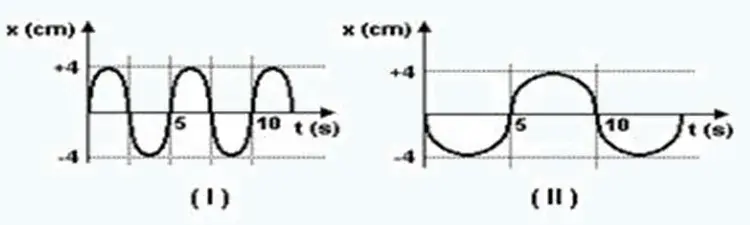
É CORRETO afirmar que os dois movimentos têm:

1. mesma freqüência, amplitudes iguais e fases diferentes.
2. freqüências diferentes, amplitudes iguais e fases diferentes.
3. mesma freqüência, amplitudes diferentes e mesma fase.
4. mesma freqüência, amplitudes iguais e mesma fase.
5. freqüências diferentes, amplitudes iguais e mesma fase.

08. (AFA) A figura abaixo apresenta os gráficos da posição (x) em função do tempo (t) para dois sistemas A e B de mesma massa m que oscilam em MHS, de igual amplitude.

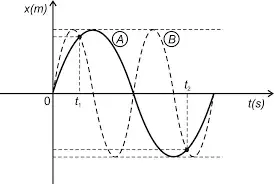
Sendo E_CA e E_CB as energias cinéticas dos sistemas A e B respectivamente no tempo t1 ; E_PA e E_PB as energias potenciais dos sistemas A e B respectivamente no tempo t₂ , é correto afirmar que

1. ECA=ECB
2. E_PA=E_PB
3. E_CA=E_CB
4. E_PB=E_PA

09. (IFSul) Uma partícula, executando um movimento harmônico simples, move-se ao longo de um eixo Ox, e sua posição, em função do tempo ao longo desse eixo é representada no gráfico da figura ao lado.

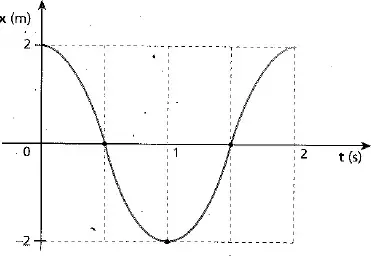
A partir da análise do gráfico, a função horária, em unidades SI, que representa corretamente o movimento harmônico simples descrito por essa partícula é

1. X = 2cos (πt)
2. X = 2sen (πt)
3. X = 4sen (πt + π)
4. X = 4cos (πt + π/2)

10. (EsPCEx) O gráfico abaixo representa a energia cinética E_c de um oscilador massa-mola ideal que descreve um movimento harmônico simples em função de sua posição x.

Podemos afirmar que na posição x = -1 m a energia cinética, em joules, do oscilador vale

1. 42
2. 45
3. 49
4. 52
5. 55