Função Horária ou do Tempo no MHS
Lista de 10 exercícios de Física com gabarito sobre o tema Função Horária ou do Tempo no MHS com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Função Horária ou do Tempo no MHS.
01. (Fuvest) Os smartphones modernos vêm equipados com um acelerômetro, dispositivo que mede acelerações a que o aparelho está submetido.
O gráfico foi gerado a partir de dados extraídos por um aplicativo do acelerômetro de um smartphone pendurado por um fio e colocado para oscilar sob a ação da gravidade. O gráfico mostra os dados de uma das componentes da aceleração (corrigidos por um valor de referência constante) em função do tempo.
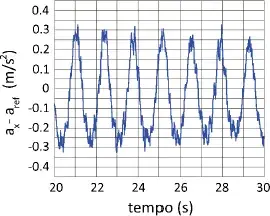
Com base nos dados do gráfico e considerando que o movimento do smartphone seja o de um pêndulo simples a ângulos pequenos, o comprimento do fio é de aproximadamente:
Note e adote:
Use π = 3.
Aceleração da gravidade: g = 10 m/s².
- 5 cm
- 10 cm
- 50 cm
- 100 cm
- 150 cm
Resposta: C
Resolução:
02. (EsPCEx) Um ponto material realiza um movimento harmônico simples (MHS) sobre um eixo 0x, sendo a função horária dada por:
x = 0,08 . cos (π/4 t + π), para x em metros e t em segundos
A pulsação, a fase inicial e o período do movimento são, respectivamente,
- π/4 rad/s, 2 π rad, 6 s.
- 2π rad, π/4 rad/s , 8 s.
- π/4 rad/s, π rad, 4 s.
- π rad/s, 2 π rad, 6 s.
- π/4 rad/s, π rad, 8 s.
Resposta: E
Resolução:
03. (UFU) O gráfico a seguir representa o movimento oscilatório de um objeto preso a uma mola.
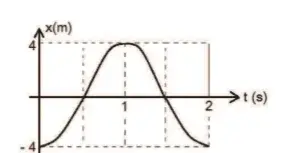
Qual das alternativas indica corretamente a função horária desse movimento harmônico?
- x = 4 cos (2π t + π).
- x = - 4 sen (π t + π).
- x = 4 cos (π t + 2π).
- x = 4 cos (π t + π).
Resposta: D
Resolução:
04. (UPE) Um gerador que produz energia a partir das ondas do mar consiste essencialmente em uma boia que sobe e desce com o movimento das ondas, fazendo um motor girar e produzir eletricidade. Com o objetivo de verificar a disponibilidade e eficiência dessa forma de geração de energia na costa pernambucana. um grupo de pesquisadores instalou uma boia no mar. Um trecho do gráfico da altura da boia y em função do tempo t é mostrado a seguir
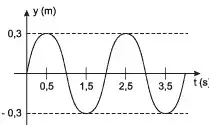
A altura foi medida em relação ao nível da água do mar sem ondas. Com base nessas:
- y(t) = (0,3 m) sen(πt)
- y(t) = (0,3 m) cos(πt)
- y(t) = (0,3 m) sen(0,5πt)
- y(t) = (30 m) sen(1,5πt)
- y(t) = (30 m) cos(1,5πt)
Resposta: A
Resolução:
A resposta correta é a (A), y(t) = (0,3 m) sen(πt).
A função y(t) = (0,3 m) sen(πt) é uma função senoidal com amplitude de 0,3 m e período de 2π segundos. Essa função é a que melhor se ajusta ao gráfico fornecido.
As demais alternativas estão incorretas:
(B): y(t) = (0,3 m) cos(πt) não é uma função senoidal, pois o valor máximo é negativo.
(C): y(t) = (0,3 m) sen(0,5πt) não é uma função senoidal, pois o período é menor do que o período do gráfico fornecido.
(D): y(t) = (30 m) sen(1,5πt) não é uma função senoidal, pois a amplitude é muito maior do que a amplitude do gráfico fornecido.
(E): y(t) = (30 m) cos(1,5πt) não é uma função senoidal, pois o valor máximo é negativo.
Explicação detalhada:
A amplitude de uma função senoidal é a distância entre o valor máximo e o valor mínimo da função. No gráfico fornecido, o valor máximo da altura da boia é de aproximadamente 0,3 m. Portanto, a amplitude da função senoidal que representa o gráfico deve ser de 0,3 m.
O período de uma função senoidal é o tempo necessário para a função completar uma oscilação completa. No gráfico fornecido, a boia completa uma oscilação completa em aproximadamente 4 segundos. Portanto, o período da função senoidal que representa o gráfico deve ser de 4 segundos.
Com base nessas informações, a função senoidal que melhor se ajusta ao gráfico fornecido é y(t) = (0,3 m) sen(πt).
Exemplo:
No gráfico fornecido, o valor da altura da boia no tempo t = 0 é de aproximadamente 0 m. Substituindo esses valores na função y(t) = (0,3 m) sen(πt), obtemos:
y(t) = (0,3 m) sen(πt)
y(0) = (0,3 m) sen(π(0))
y(0) = (0,3 m) sen(0)
y(0) = 0 m
Como o valor calculado é igual ao valor observado no gráfico, podemos concluir que a função y(t) = (0,3 m) sen(πt) é a que melhor representa o gráfico fornecido.
05. (PUC-RS) Ao visitar o Panteon, em Paris, Tales conheceu o Pêndulo de Foucault. O esquema abaixo indica a posição do pêndulo fixado a uma haste horizontal, num certo instante.
Sendo L o seu comprimento e x o ângulo em relação a sua posição de equilíbrio, então a altura h do pêndulo em relação à haste horizontal é expressa pela função
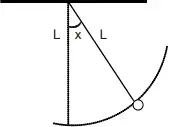
- h(x) = L cos (x)
- h(x) = L sen (x)
- h(x) = L sen (2x)
- h(x) = L cos (2x)
- h(x) = 2L cos (x)
Resposta: A
Resolução: A altura ℎ do pêndulo em relação à haste horizontal é uma função do ângulo x em relação à sua posição de equilíbrio. No caso de um pêndulo simples, a relação entre ℎ, x, e o comprimento da haste L é dada por: h(x) = L cos (x)
06. (EN) Analise o gráfico abaixo.
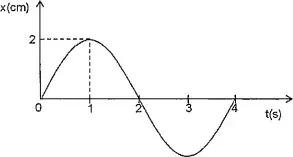
O gráfico acima representa a posição x de uma partícula que realiza um MHS (Movimento Harmônico Simples), em função do tempo t.
A equação que relaciona a velocidade v, em cm/s, da partícula com a sua posição x é
- v² = π² (1 - x²)
- v² = π²/2 (1 - x²/2)
- v² = π² (1 + x²)
- v² = π² (1 - x²/4)
- v² = π²/4 (1 - x²)
Resposta: D
Resolução:
07. (UFV-MG) Duas partículas descrevem movimentos harmônicos simples representados nos gráficos (I) e (II) a seguir.
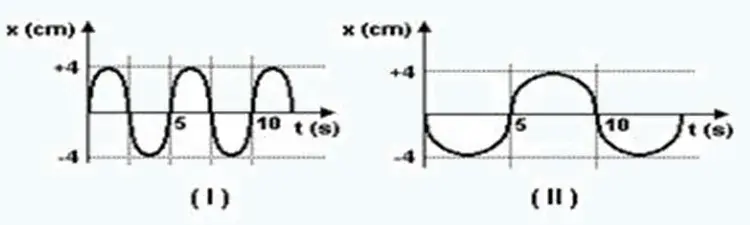
É CORRETO afirmar que os dois movimentos têm:
- mesma freqüência, amplitudes iguais e fases diferentes.
- freqüências diferentes, amplitudes iguais e fases diferentes.
- mesma freqüência, amplitudes diferentes e mesma fase.
- mesma freqüência, amplitudes iguais e mesma fase.
- freqüências diferentes, amplitudes iguais e mesma fase.
Resposta: B
Resolução:
Observando os gráficos (I) e (II) de dois movimentos harmônicos simples (MHS), podemos fazer as seguintes observações:
1. Frequência: A frequência de um MHS é determinada pelo número de ciclos completos (oscilações) que ocorrem em um determinado período de tempo. No gráfico (I), podemos ver que o movimento completa mais ciclos no mesmo intervalo de tempo em comparação com o gráfico (II). Portanto, os dois movimentos têm frequências diferentes.
2. Amplitude: A amplitude é a máxima distância da partícula à sua posição de equilíbrio. Ambos os gráficos indicam amplitudes iguais, pois a maior distância do ponto zero (posição de equilíbrio) é a mesma nos dois casos.
3. Fase: A fase de um MHS é determinada pelo deslocamento inicial no ciclo. No gráfico (I), a partícula começa a oscilação em sua posição de equilíbrio, enquanto no gráfico (II), a partícula começa sua oscilação em um ponto mais distante do ponto de equilíbrio. Portanto, as fases iniciais são diferentes.
Com base nas observações acima, podemos concluir que os dois movimentos têm:
Freqüências diferentes, amplitudes iguais e fases diferentes.
08. (AFA) A figura abaixo apresenta os gráficos da posição (x) em função do tempo (t) para dois sistemas A e B de mesma massa m que oscilam em MHS, de igual amplitude.
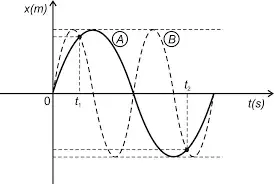
Sendo ECA e ECB as energias cinéticas dos sistemas A e B respectivamente no tempo t1 ; EPA e EPB as energias potenciais dos sistemas A e B respectivamente no tempo t2 , é correto afirmar que
- ECA=ECB
- EPA=EPB
- ECA=ECB
- EPB=EPA
Resposta: D
Resolução:
09. (IFSul) Uma partícula, executando um movimento harmônico simples, move-se ao longo de um eixo Ox, e sua posição, em função do tempo ao longo desse eixo é representada no gráfico da figura ao lado.
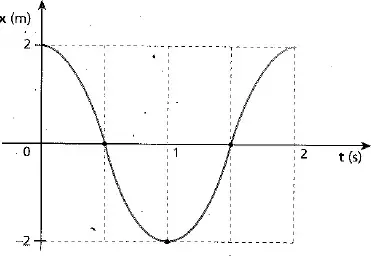
A partir da análise do gráfico, a função horária, em unidades SI, que representa corretamente o movimento harmônico simples descrito por essa partícula é
- X = 2cos (πt)
- X = 2sen (πt)
- X = 4sen (πt + π)
- X = 4cos (πt + π/2)
Resposta: A
Resolução:
10. (EsPCEx) O gráfico abaixo representa a energia cinética Ec de um oscilador massa-mola ideal que descreve um movimento harmônico simples em função de sua posição x.
Podemos afirmar que na posição x = -1 m a energia cinética, em joules, do oscilador vale

- 42
- 45
- 49
- 52
- 55
Resposta: B
Resolução: