Sistema Massa Mola no MHS
Lista de 10 exercícios de Física com gabarito sobre o tema Sistema Massa Mola no MHS com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.
01. (UEFS) A figura representa um sistema massa-mola ideal, cuja constante elástica é de 4 N/cm.
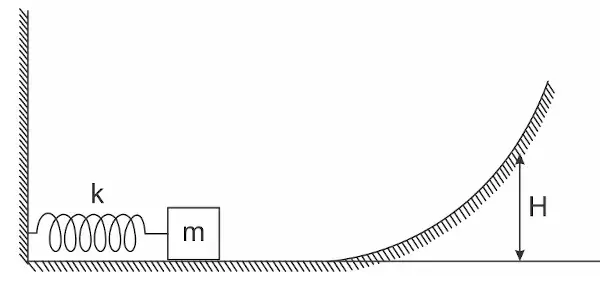
Um corpo de massa igual a 1,2 kg é empurrado contra a mola, comprimindo-a de 12,0 cm. Ao ser liberado, o corpo desliza ao longo da trajetória representada na figura. Desprezando-se as forças dissipativas em todo o percurso e considerando a aceleração da gravidade igual a 10 m/s², é correto afirmar que a altura máxima H atingida pelo corpo, em cm, é igual a:
- 24
- 26
- 28
- 30
- 32
02. (UERJ) Uma empresa testou quatro molas para utilização em um sistema de fechamento automático de portas. Para avaliar sua eficiência, elas foram fixadas a uma haste horizontal e, em suas extremidades livres, foram fixados corpos com diferentes massas
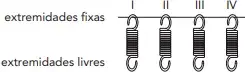
Observe na tabela os valores tanto das constantes elásticas K das molas quanto das massas dos corpos.
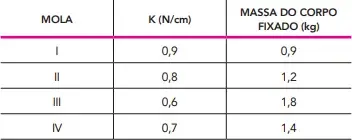
Para que o sistema de fechamento funcione com mais eficiência, a mola a ser utilizada deve ser a que apresentou maior deformação no teste.
Essa mola está identificada pelo seguinte número:
- I
- II
- III
- IV
03. (Unipam) Um pêndulo simples e sistema massa-mola têm na Terra períodos iguais a T1 e T2, respectivamente. Suponha que esses pêndulos sejam levados para a Lua, onde a aceleração da gravidade é cerca de 1/6 da aceleração da gravidade terrestre. Com relação aos períodos dos pêndulos na Terra e na Lua, marque a alternativa correta.
- Tanto o período do pêndulo quanto o do sistema massa-mola não se alteram.
- Tanto o período do pêndulo quanto o do sistema massa-mola serão maiores na Lua do que na Terra.
- O período do pêndulo será maior na Lua e o do sistema massa-mola não se altera.
- O período do pêndulo será maior na Lua e o do sistema massa-mola será menor na Lua.
04. (UEFS)
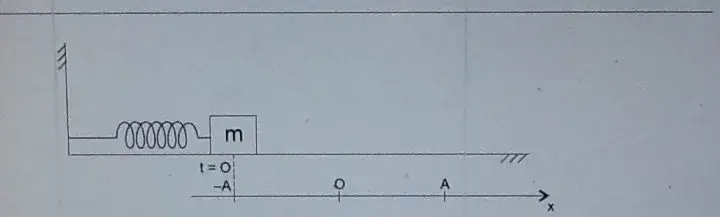
Um corpo com massa de 30,0g é preso na extremidade livre de uma mola comprimida, cuja constante elástica é igual a 0,27N/m. Depois de abandonado na posição x = −A, oscila, periodicamente, em torno da posição de equilíbrio, conforme a figura.
Sabendo-se que a mola foi comprimida de modo a armazenar no sistema massa-mola energia de 1,35.10−3J e desprezando-se as forças dissipativas, é correto afirmar:
- O período do movimento é de (3π/2)s.
- A pulsação da oscilação é de 2,0rad/s.
- A energia mecânica do corpo na posição x = A/2 é 50% potencial e 50% cinética.
- A energia cinética do corpo, ao passar pela posição de equilíbrio, tem valor igual a zero.
- O corpo ocupa a posição x = 10,0cm à direita da posição de equilíbrio, no instante t = (π/3)s.
05. (UEMA) A aceleração da gravidade pode ser determinada de várias maneiras como, por exemplo, pela queda livre, pelo sistema massa-mola na vertical, ou, até mesmo, por um pêndulo simples.
Se um pêndulo simples na Terra tem um período de oscilação igual a 1s, o valor da gravidade, em m/s², de um planeta “X” em que o período desse pêndulo passa a ser de 2s é igual a [Dado: g=10m/s²(gravidade da Terra)].
- 0,4.
- 1,5.
- 2,5.
- 5,0.
- 40,0.
06. (EN) Oberve a figura a seguir.
Na figura acima, a mola possui uma de suas extremidades presa ao teto e a outra presa a um bloco. Sabe-se que o sistema massa-mola oscila em MHS segundo a função y(t) = 5,0sen(20t), onde y é dado em centímetros e o tempo em segundos.
Qual a distensão máxima da mola, em centímetros? Dados: g = 10m/s²
- 5,5
- 6,5
- 7,5
- 8,5
- 9,5
07. (PUC-PR) O movimento harmônico simples (MHS) pode ser usado para representar alguns fenômenos periódicos como o pêndulo simples, sistema massa-mola e ainda a vibração entre átomos.
As equações do movimento surgem da projeção de um movimento circular uniforme sobre um dos eixos.
A figura a seguir representa um ponto descrevendo um movimento circular uniforme com velocidade escalar de 8 m/s em um sistema de eixos cartesianos.
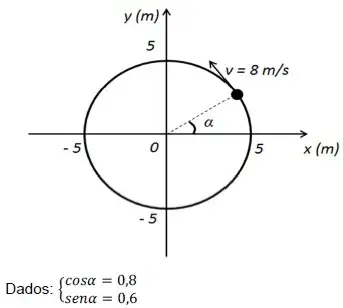
A partir da figura e das informações citadas, calcule o módulo das projeções sobre o eixo x da velocidade e aceleração do movimento.
- 8 m/s e 5 m/s²
- 4,8 m/s e 10,24 m/s²
- 10,24 m/s e 8 m/s²
- 8 m/s e 8 m/s²
- 4,8 m/s e 6,4 m/s²
08. (IFBA) Um sistema massa-mola é posto para oscilar, numa superfície horizontal sem atrito, realizando um movimento harmônico simples (MHS), de modo que sua posição no tempo obedece à equação no S.I.:
x(t) = 5, 0.cos (2π.t + π/2)
Quando o tempo de oscilação for de 4,0 s, sua posição será igual a:
- 9,0
- 7,0
- 5,0
- 2,0
- 0,0
09. (UECE) Em um sistema massa-mola, um objeto oscila de modo que sua posição seja dada por x = A cos(2ƒt), onde A é uma constante com dimensão de comprimento, x é a posição, ƒ a frequência e t o tempo. A maior extensão do trajeto que o objeto percorre em um ciclo é
- A/2.
- A.
- 2A.
- 2πƒ.
10. (EsPCEx) Uma mola ideal está suspensa verticalmente, presa a um ponto fixo no teto de uma sala por uma de suas extremidades. Um corpo de massa 80 g é preso à extremidade livre da mola e verifica-se que a mola desloca-se para uma nova posição de equilíbrio. O corpo é puxado verticalmente para baixo e abandonado de modo que o sistema massa-mola passa a executar um movimento harmônico simples. Desprezando as forças dissipativas, sabendo que a constante elástica da mola vale 0,5 N/m e considerando π = 3,14, o período do movimento executado pelo corpo é de:
- 1,256 s
- 2,512 s
- 6,369 s
- 7,850 s
- 15,700 s