EsPCEx 2021: Matemática
01. (ESPCEX) Considere a função p :ℝ→ℝ dada por p(x)=x⁵– 5 x⁴+10 x³– 10x² + 5x – 1 e a função q: ℝ→ℝ onde q (x)=p(x – 2000). O valor numérico de q (2021) é igual a
- 2.021.000
- 2.021.320
- 3.200.000
- 3.202.021
- 4.084.101
02. (ESPCEX) O Cap R. Gomes é um autêntico “canga”, isto é, um militar que não apenas coopera com os membros de sua equipe, mas estimula superiores, pares e subordinados ao bom cumprimento das missões. Em particular, ele incentiva um grupo de militares a melhorar o desempenho na corrida.
Para tal, criou um programa de treinamento em que é preciso correr exatamente 576 Km no total, começando com 26 Km na primeira semana e, a partir da segunda, acrescentando exatos 4 Km a cada semana, ou seja, cada integrante do grupo deve correr exatamente 26 Km na 1a semana, 30 Km na 2ª semana, 34 Km na 3ª semana e assim sucessivamente.
Após quantas semanas a meta de 576 Km será atingida?
- 10
- 11
- 12
- 13
- 14
03. (ESPCEX) Sejam x um ângulo qualquer, em radianos, e i a unidade imaginária. O determinante da matriz 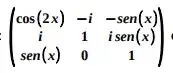 é igual a
é igual a
- −i.
- i.
- −1.
- 1.
- 0.
04. (ESPCEX) Simplificando-se a expressão 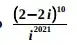 , onde i é a unidade imaginária, obtém-se
, onde i é a unidade imaginária, obtém-se
- −2¹⁵ i.
- 2¹⁵.
- −2¹⁰.
- −2¹⁵.
- 2¹⁵ i.
05. (ESPCEX) Considere i a unidade imaginária. A soma infinita 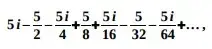 onde o n-ésimo termo é dado por
onde o n-ésimo termo é dado por 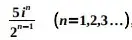 resulta no número complexo cujas partes real e imaginária são, respectivamente, iguais a
resulta no número complexo cujas partes real e imaginária são, respectivamente, iguais a
- 2 e 4.
- 2 e – 4.
- – 4 e 2.
- 4 e – 2.
- – 2 e 4.
06. (ESPCEX) O número de soluções inteiras que satisfaz a inequação 4ˣ−10⋅2ˣ+16 < 0 é igual a
- 4.
- 3.
- 2.
- 1.
- 0.
07. (ESPCEX) O produto o (log3 12)⋅[log4 (10log10 7 )]⋅[log12(log11 114 )]⋅(log7 81) é igual a
- 3.
- 4.
- 5.
- 6.
- 7.
08. (ESPCEX) O número de soluções, em ℝ, da equação |x+2|+|x−1|=x+1 , é igual a
- 0.
- 1.
- 2.
- 3.
- 4.
09. (ESPCEX) Quais as medidas, em centímetros, dos lados do retângulo de maior área que está contido em um triângulo equilátero de lado 8 cm, estando a base do retângulo situada num lado desse triângulo?
- 2 e 3√2
- 4 e √3
- 4 e 3√2
- 2 e 2√3
- 4 e 2√3
10. (ESPCEX) Calculando-se o volume de uma esfera circunscrita a um cone equilátero cujo raio da base mede √3 cm, obtém-se

11. (ESPCEX) Um aluno da EsPCEx tem a probabilidade de 60% de acertar um problema de Matemática ao tentar resolvê-lo. Numa prova de Matemática com 5 problemas, qual a probabilidade desse aluno acertar ao menos um dos 5 problemas?
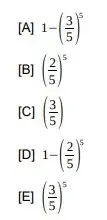
12. (ESPCEX) Dado um dodecaedro regular, exatamente, quantas retas ligam dois de seus vértices mas não pertencem a uma mesma face desse dodecaedro?
- 60
- 100
- 130
- 160
- 190
13. (ESPCEX) Foi realizada em uma escola uma pesquisa que gerou as seguintes informações:
- 30 alunos leem os livros A, B e C;
- 60 alunos leem os livros A e C;
- 40 alunos leem os livros B e C;
- 40 alunos leem os livros A e B;
- 150 alunos leem o livro A;
- 60 alunos leem somente o livro B;
- 90 alunos leem o livro C; e
- 120 alunos não leem livro nenhum.
De posse dessas informações, o número total de alunos que responderam a pesquisa é igual a
- 310.
- 350.
- 360.
- 390.
- 420.
14. (ESPCEX) Abaixo temos 3 proposições:

Analisando as proposições acima, podemos afirmar que
- I é a única proposição verdadeira.
- I e III são as únicas proposições verdadeiras.
- todas as proposições são verdadeiras.
- nenhuma proposição é verdadeira.
- II e III são as únicas proposições verdadeiras.
15. (ESPCEX) Os valores de x real que satisfazem à equação 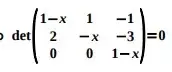 pertencem ao conjunto
pertencem ao conjunto
- (−∞,3].
- (3,7].
- (7,11].
- (11,15].
- (15,+∞).
16. (ESPCEX) Dado o sistema linear 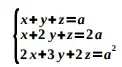 os valores do número real a , tais que o sistema linear acima tenha solução, pertencem ao conjunto
os valores do número real a , tais que o sistema linear acima tenha solução, pertencem ao conjunto
- (−∞,−1].
- (−1 ,4].
- (4 ,8].
- (8,11].
- (11,+∞).
17. (ESPCEX) A circunferência que tem seu centro no ponto (1 ,−1) e é tangente à reta de equação Y=3/4 x+2 tem equação dada por
- x²+ y²−2 x+2 y−7=0.
- x²+ y²−2 x−2 y−7=0.
- x²+ y²+2 x+2 y+7=0.
- x²+ y²−2x−2 y+7=0.
- x²+ y²−2 x+2 y=0.
18. (ESPCEX) Dado um cubo, o número de pares distintos de retas reversas que podemos traçar, de tal forma que cada reta contenha uma aresta desse cubo, é igual a
- 24.
- 30.
- 36.
- 42.
- 48.
19. (ESPCEX) Considere o triângulo ABC de vértices nos pontos A(1,2) , B(9,6) e C(3,8). Sabendo que o ponto I(a , b) pertence ao lado AB e é o segmento correspondente à altura do triângulo ABC relativa ao lado AB , o valor de a+b é igual a
- 5.
- 7.
- 9.
- 11.
- 13.
20. (ESPCEX) Considere a função f :[−1 ,+∞)→[−7 ,+∞) , onde f (x)=x²+2 x−6 . Sabendo que a função f tem uma inversa f⁻¹ e sendo I(a , b) o ponto de interseção dos gráficos de f e f⁻¹, a soma a+b pertence ao intervalo
- (−∞,0 ].
- (0 ,5 ].
- (5 ,10 ].
- (10,15].
- (15 ,+∞).