FAMEMA2024:
36. (FAMEMA 2024) Uma sequência engraçada que já foi muitas vezes explorada em comédias e desenhos animados tem como cenário as estruturas em aço de edifícios. Nessa sequência, um personagem, sonâmbulo, caminha sobre uma viga da estrutura de um prédio. Quando o personagem está prestes a cair, uma outra viga, que está sendo erguida por um guindaste, nivela-se com a primeira, possibilitando que o próximo passo não seja no vazio. O personagem passa, então, a caminhar sobre essa viga que está subindo e, novamente, quando tudo parece que vai dar errado, a viga em ascensão nivela-se com a outra viga do próximo andar, garantindo a continuidade da caminhada. 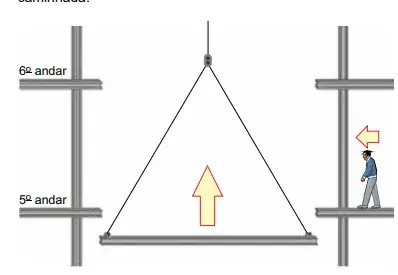
Admita que a viga em ascensão meça 30 m de comprimento, se mantenha sempre na horizontal e realize movimento uniforme; que a velocidade do sonâmbulo seja constante e de valor igual a 0,5 m/s; que a altura entre as vigas de um andar e do próximo seja de 3 m. Considerando a sequência de acontecimentos descritos, a velocidade com que a viga em ascensão se movimenta é de
- 0,05 m/s.
- 0,30 m/s.
- 0,50 m/s.
- 0,25 m/s.
- 0,10 m/s.
Resposta: A
Resolução:
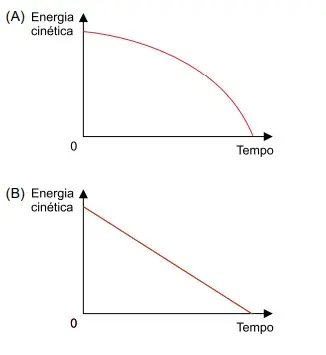
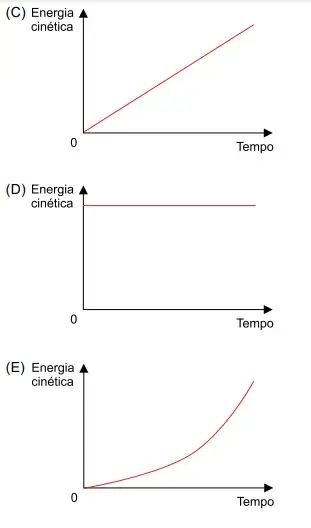
37. (FAMEMA 2024) Um corpo dotado de rodinhas ideais, inicialmente em repouso, e apoiado sobre uma superfície plana, horizontal e livre de atritos, passa a receber a ação de uma força resultante horizontal, de direção, sentido e intensidade constantes. O esboço do gráfico que corresponde à variação da energia cinética desse corpo em função do tempo é:
Resposta: E
Resolução:
38. (FAMEMA 2024) No painel dos carros a combustão interna, uma lâmpada de advertência se acende quando a temperatura do líquido de arrefecimento do motor chega a 115 ºC. Esse líquido é uma mistura que tem calor específico igual a 0,6 cal/(g × ºC) e sua densidade pode ser igualada à da água, que é de 1000 g/L.
Considere um veículo que usa 10 L de líquido de arrefecimento para manter a temperatura do motor controlada. Em uma eventual falha no processo de resfriamento desse líquido, a menor quantidade de calor acumulada para que, a partir da temperatura de 15 ºC, a luz de advertência se acenda é de
- 750 kcal.
- 1200 kcal.
- 600 kcal.
- 1500 kcal.
- 300 kcal.
Resposta: C
Resolução:
39. (FAMEMA 2024) O índice de refração relativo nA,B entre dois meios, A e B, é 0,5. Sabendo que o índice de refração absoluto do meio A vale 2, o índice absoluto do meio B tem valor igual a
- 5.
- 2.
- 1.
- 10.
- 4.
Resposta: E
Resolução:
40. (FAMEMA 2024) Um aquecedor elétrico é construído com 4 resistores ôhmicos de mesmo valor de resistência elétrica cada um. Os fios de ligação e o gerador são ideais. A potência elétrica total original tem valor Pot e o circuito elétrico é o indicado na figura. 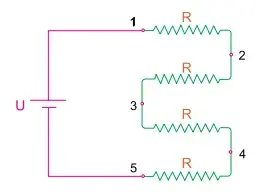
Um pedaço de fio, ideal, é soldado ao circuito, nos pontos indicados pelos números 2 e 3. Promovida essa alteração, a nova potência elétrica total dissipada pelo aquecedor passa a ser
- 3/2 x Pot
- 2/3 x Pot
- 1/2 x Pot
- 4/3 x Pot
- 1/3 x Pot
Resposta: D
Resolução: