FMJ 2024: Matemática

11. (FMJ 2024) Em uma autoescola, 65% dos alunos passaram na prova prática na primeira tentativa e 80% dos que não passaram na primeira tentativa passaram na segunda. Após essas duas tentativas, o total de alunos aprovados na prova prática foi 651 e o total de alunos não aprovados foi

1. 49.
2. 99.
3. 149.
4. 199.
5. 249.

Começa em 3:13

12. (FMJ 2024) Uma loja de carros antigos separou 12 veículos para que os clientes pudessem testá-los. As chaves dos 12 veículos foram colocadas em uma mesma gaveta, mas sem identificação, por isso um funcionário deve tentar ligar os carros com as chaves e, se uma chave ligar um carro, a chave será colocada no porta-luvas do respectivo carro.

As chaves são muito parecidas, logo não será possível identificar um par carro-chave apenas com inspeção visual. O funcionário irá testar as chaves em um carro por vez e, para um mesmo carro, não será necessário testar todas as chaves, pois, após testar todas as chaves menos uma, aquela não testada será a chave certa; por exemplo, se sobrarem 5 chaves, em no máximo 4 tentativas a chave correta do carro em teste será determinada.

Com muita sorte, esse funcionário poderá terminar a tarefa após 11 tentativas, pois, se ele obtiver sucesso em ligar cada um dos 11 primeiros carros na primeira tentativa, a 12ª chave será do carro ainda não testado. Por outro lado, existirá a possibilidade de, para cada carro, sempre ser necessário testar todas as chaves restantes menos uma. Nesse caso infortunoso, o número de tentativas será

1. 72.
2. 66.
3. 78.
4. 132.
5. 144.

Começa em 6:50

13. (FMJ 2024) Uma campanha publicitária irá distribuir 400 ingressos para um espetáculo, sendo 120 ingressos especiais e os demais ingressos comuns.

A distribuição dos ingressos será feita no estande da campanha, com os ingressos sendo depositados em uma urna e cada interessado pegando aleatoriamente um ingresso.

A probabilidade de o primeiro ingresso especial ser retirado pela segunda pessoa a pegar um ingresso é

1. 3/10
2. 3/5
3. 4/19
4. 1/12
5. 2/15

Começa em 9:30

14. (FMJ 2024) Hoje, a soma das idades de 4 filhos é igual ao dobro da idade do pai. Isidoro, o filho mais velho, tem 16 anos a mais do que Felipe, o mais novo. Quando os gêmeos Gustavo e Henrique nasceram, o pai tinha o triplo da idade que Isidoro tinha e, quando Felipe nasceu, Gustavo e Henrique tinham 4 anos.

Hoje, a idade de Felipe, em anos, está compreendida entre

1. 25 e 30.
2. 35 e 40.
3. 30 e 35.
4. 15 e 20.
5. 20 e 25.

Começa em 13:15

15. (FMJ 2024) A reta r passa pela origem de um sistema de coordenadas xy e intersecta a reta s no ponto de coordenadas (3, 2).

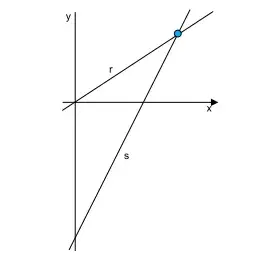
Sabendo que o coeficiente angular da reta s vale o triplo do coeficiente angular da reta r, a equação da reta s é

1. y = 6x – 16
2. y = x – 1
3. y = 3x – 7
4. y = 4x – 10
5. y = 2x – 4

Começa em 15:15

16. (FMJ 2024) A constante real k satisfaz a equação

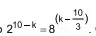
Considerando log10 5 = 0,7 e log10 8 = 0,9, o valor de n que satisfaz a equação log10 k² = log10 64n – 4,4 é

1. 1.
2. 10000.
3. 10.
4. 100.
5. 1000.

Começa em 19:00

17. (FMJ 2024) Um dos lados de um retângulo foi dividido por um ponto em 2 partes de mesma medida, e o lado oposto foi dividido por dois pontos em 3 partes de mesma medida.

Dois segmentos de reta, conectando vértices do retângulo com os pontos que dividiram os lados do retângulo, determinaram um triângulo de área 3 cm², destacado na figura.

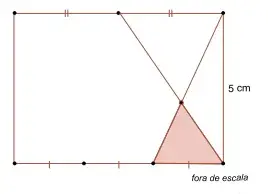
Observando que um dos lados do retângulo mede 5 cm, seu perímetro é igual a

1. 22 cm.
2. 24 cm.
3. 26 cm.
4. 28 cm.
5. 30 cm.

Começa em 23:15

18. (FMJ 2024) Um ponto B está sobre o lado PA de um triângulo retângulo PAQ e um ponto C determina o triângulo retângulo PBC e o retângulo ABCD, conforme mostra a figura, em que as medidas das hipotenusas dos triângulos são dadas em cm.

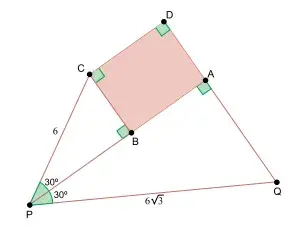
A área do retângulo ABCD é

1. 6(9 - √3) cm²
2. 9(6 - √3) cm²
3. 9(3 - √3) cm²
4. 6(6 - √3) cm²
5. 6(3 - √3) cm²

Começa em 26:10

19. (FMJ 2024) A base de um prisma reto é um triângulo isósceles com lados medindo 10 cm, 10 cm e 16 cm. Sendo o volume desse prisma igual a 1200 cm³, sua área lateral é

1. 900 cm².
2. 800 cm².
3. 1000 cm².
4. 1200 cm².
5. 600 cm².

Começa em 29:00

20. (FMJ 2024) Em uma linguagem de programação natural, a função TROCALETRAS(“PALAVRA”, p, q) tem como parâmetros uma PALAVRA qualquer e dois números inteiros p e q, que devem ser maiores ou iguais a 1, diferentes entre si e menores ou iguais ao número de letras da palavra recebida.

Essa função retorna uma nova palavra, em que a primeira letra é a letra que está na posição p da palavra recebida, a segunda letra é a letra que está na posição q da palavra recebida e as demais letras são as letras restantes na ordem em que estavam.

Por exemplo, ao executarmos TROCALETRAS(“AMOR”, 1, 3) a função retorna AOMR e ao executarmos TROCALETRAS(“AMOR”, 4, 1) a função retorna RAMO. A palavra recebida pela função pode ser o retorno de uma palavra gerada pela própria função, nesse caso, primeiro é executada a função que aparece dentro dos parênteses e depois a função fora dos parênteses é aplicada na palavra gerada. A palavra final resultante ao executarmos TROCALETRAS(TROCALETRAS(“SORTE”, 2, 5), 5, 2) é

1. SORTE.
2. RESTO.
3. RETOS.
4. ERTOS.
5. TEOSR.