ITA 2024:
Gabarito: B
37. (ITA 2024) Sejam A, B, C ⊆ R tais que C ⊆ A. Considere as afirmações:
I. (A ∩ B) ∪ C = A ∩ (B ∪ C).
II. A ∩ B = C ∪ (B ∩ (R − C)).
III. A ∩ (B − C) = (A ∩ B) − C.
É (São) VERDADEIRA(S):
- apenas I e II.
- apenas I e III.
- apenas II.
- apenas III.
- I, II e III.
Gabarito: E
38. (ITA 2024) Sejam A; B; C; D ∈ Mn(R). Considere o sistema linear 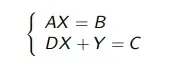
nas variáveis X; Y ∈ Mn(ℝ). Considere as afirmações:
I. Se det A = 0 ou det D = 0, então o sistema é impossível.
II. Se A = B, então o sistema possui uma única solução.
III. O sistema possui uma única solução apenas se A e D são inversíveis.
É (São) VERDADEIRA(S):
- apenas I.
- apenas II.
- apenas III.
- apenas II e III.
- nenhuma.
Gabarito: A
39. (ITA 2024) Determine o valor de 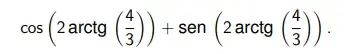
- 17/25
- 4/5
- 24/25
- 28/25
- 31/25
Gabarito: B
40. (ITA 2024) Considere o conjunto:
A = {1; 2; 4; 8; 16; 32; 64; 128; 256}:
Qual o menor n ∈ ℕ tal que todo subconjunto de A com n elementos contenha pelo menos
um par cujo produto seja 256?
- n = 5.
- n = 6.
- n = 7.
- n = 8.
- n = 9.
Gabarito: D
41. (ITA 2024) Considere o conjunto C = {1; 2; 3; 4; 5}. Para cada escolha possível de a0, a1, a2, a3, a4 ∈ C, dois a dois distintos, formamos o polinômio
a0 + a1x + a2x² + a3x³ + a4x⁴:
A soma das raízes, contadas com multiplicidade, de todos os polinômios formados nesse processo é igual a:
- − 17125/4.
- −1800.
- −360.
- − 351/2.
- − 101/4.
Gabarito: C
42. (ITA 2024) O valor de k ∈ R de modo que as raízes do polinômio p(x) = x³ + 3x² −6x + k estejam em progressão geométrica é:
- −18.
- −16.
- −8.
- −2.
- −1.
Gabarito: E
43. (ITA 2024) Considere um cilindro circular reto tal que a área da sua base A1, a área da sua superfície lateral A2 e o seu volume A3 formem, nesta ordem, uma progressão geométrica crescente. A medida do raio da base pode estar no intervalo:
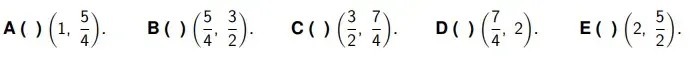
Gabarito: D
44. (ITA 2024) Um poliedro convexo tem 24 vértices e 36 arestas.
Sabemos que cada vértice une 3 faces e que o número de arestas em cada face só pode assumir um entre dois valores m ou n. É CORRETO afirmar que:
- é possível que m = 3 e n = 4.
- é possível que m = 3 e n = 5.
- é possível que m = 3 e n = 7.
- é possível que m = 3 e n = 8.
- é possível que m = 4 e n = 5.
Gabarito: C
45. (ITA 2024) Considere um triângulo ABC e M o ponto médio do lado BC. Tome o ponto R 6= A na reta AB tal que m(AB) = m(BR) e o ponto Q na reta AC tal que m(AC) = 2 m(CQ) e Q não esteja no segmento AC. A reta RM corta o lado AC no ponto S e a reta QM corta o lado AB no ponto P.
Sendo 24 a área do triângulo ABC, o valor da área do quadrilátero APMS vale:
- 15.
- 16.
- 17.
- 18.
- 19.
Gabarito: D
46. (ITA 2024) Sejam a = 1+3√ 3i e b = 2√ 3+4i números complexos. O menor valor m ∈ N tal que a m = b m é:
- 6.
- 8.
- 10.
- 12.
- não existe m ∈ ℕ satisfazendo esta igualdade.
Gabarito: A
47. (ITA 2024) Considere o triângulo de vértices 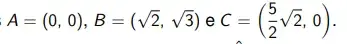 .
.
A equação da reta que passa por B e é perpendicular à bissetriz do ângulo ABC é:

Gabarito: C
48. (ITA 2024) Considere a elipse dada pela equação
&3164; λx² + (λ + 4)y² − 4λx − (10λ + 40)y + 25(λ + 4) − λ² = 0;
e o círculo de equação
x² + y² − 4x − 12y + 36 = 0:
Estando o interior do círculo inteiramente contido no interior da elipse, o valor de – ∈ R − {−4; 0} quando a excentricidade da elipse é máxima é igual a:
- 3.
- 5.
- 9.
- 13.
- 15