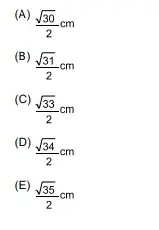Santa Casa 2024:

Gabarito: C

71. (Santa Casa) Os dois primeiros termos de uma progressão aritmética são a₁ = 7/3 a a₂ 25/12. A soma dos 20 primeiros termos dessa progressão aritmética é igual a

1. - 6/7
2. - 8/9
3. - 5/6
4. - 7/8
5. - 9/10

Gabarito: B

72. (Santa Casa) Certa loja emprega somente estoquistas e vendedores. O número de estoquistas dessa loja corresponde a 25% do total de empregados, sendo os demais, vendedores. Entre os estoquistas, todos recebem salários iguais, e entre os vendedores os salários também são os mesmos, sendo que o salário de um estoquista corresponde a 75% do salário de um vendedor. Se o salário dos estoquistas for aumentado em 20% e o salário dos vendedores for aumentado em 10%, o salário médio dos empregados nessa loja aumentará em

1. 13%.
2. 12%.
3. 15%.
4. 14%.
5. 11%.

Gabarito: A

73. (Santa Casa) Em um conjunto de bolas de sinuca há 15 bolas numeradas de 1 a 15. As bolas numeradas de 9 a 15 são listradas, as demais não. Tomando-se aleatoriamente uma bola listrada e uma bola não listrada, a probabilidade de a soma dos números nessas duas bolas ser maior ou igual a 18 é de

1. 3/8
2. 2/5
3. 7/20
4. 17/40
5. 9/16

Gabarito: E

74. (Santa Casa) No plano cartesiano, a parábola de equação y = 1/4 x² + 3 e a reta r de equação y = x + 3 se intersectam no ponto Q de coordenadas (0, 3), e no ponto P, como na figura

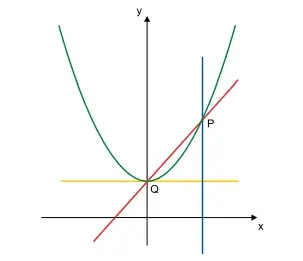
O triângulo delimitado pela reta r, pela reta horizontal que passa por Q e pela reta vertical que passa por P tem área

1. 7.
2. 9.
3. 10.
4. 11.
5. 8.

Gabarito: D

75. (Santa Casa) Considere, no plano cartesiano, o ponto P dado pela interseção do gráfico da função exponencial f(x) = 2x com a reta horizontal de equação y = 700/27. Usando os valores log2 3 = 1,58, log2 5 = 2,32 e log2 7 = 2,8, a abscissa do ponto P é

1. 4,8.
2. 4,5.
3. 4,9.
4. 4,7.
5. 4,6.

Gabarito: C

76. (Santa Casa) Na figura, o perímetro do polígono ABCDE é 15 cm, os segmentos de reta são pararelos e os pontos A, E e F são colineares.

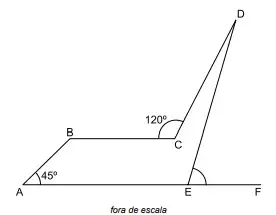
Considerando os dados contidos na figura e que AB = 1 cm, BC = 2 cm, CD = 3 cm e AE = 4 cm, o seno do ângulo DÊF é

Gabarito: C

77. (Santa Casa) No triângulo ABC, o ponto P foi tomado sobre o lado AC, como na figura, de modo que AP/PC = 9/5.

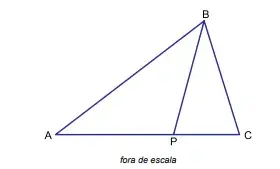
Sabendo que a área do triângulo ABC é 7 cm² e que AB = 6 cm, a altura do triângulo ABP em relação ao lado AB é

1. 1,4 cm.
2. 1,3 cm.
3. 1,5 cm.
4. 1,6 cm.
5. 1,7 cm.

Gabarito: A

78. (Santa Casa) Na figura, vê-se uma forma geométrica em vermelho que foi obtida pela junção de um setor circular de raio 3 cm e ângulo 90º com um setor de uma coroa circular de raio interno 3 cm, raio externo 4 cm e ângulo 270º.

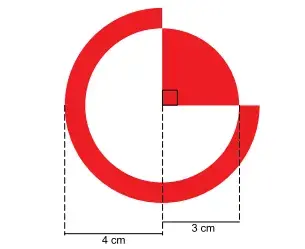
O círculo cuja área é igual à área da forma geométrica em vermelho tem raio igual a

Gabarito: B

79. (Santa Casa) A pirâmide da figura tem vértice V e base quadrada ABCD de lado medindo 6 cm. O ponto P é obtido pela projeção ortogonal do vértice V sobre o plano que contém a base ABCD.

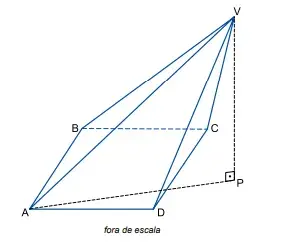
Sabendo que a pirâmide tem volume 120 cm³ e que a distância entre os pontos A e P é de 12 cm, a tangente do ângulo VÂP é igual a

1. 7/8
2. 5/6
3. 9/10
4. 8/9
5. 6/7

Gabarito: B

80. (Santa Casa) Para a realização de uma prova de matemática, uma determinada turma foi dividida em dois grupos, A e B, de modo que, para cada 3 alunos no grupo A, há 5 alunos no grupo B. A média das notas na prova de matemática dos alunos no grupo A foi 5,6 e a média das notas no grupo B foi 6,4. A média das notas de todos os alunos da turma nessa prova de matemática foi

1. 6,2.
2. 6,1.
3. 5,9.
4. 6,0.
5. 6,3.