Santa Casa 2023: Matemática

71. (Santa Casa)Sejam T_C, T_F e T_K a mesma temperatura nas escalas Celsius, Fahrenheit e Kelvin, respectivamente. As fórmulas usuais de conversão entre T_C, T_F e T_K são:

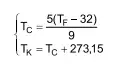
Uma fórmula que converte diretamente T_K em T_F é:

1. T_F = 1,8T_K - 523,67
2. T_F = 0,56T_K - 290,75
3. T_F = 1,8T_K - 459,67
4. T_F = 0,56T_K - 305,15
5. T_F = 1,8T_K - 533,15

72. (Santa Casa) A tabela indica o orçamento anual destinado à saúde de três países e as conversões de suas respectivas moedas em reais

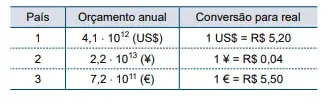
A soma do orçamento anual destinado à saúde desses três países, em reais, é igual a

1. 1,489 ⋅ 10¹⁴
2. 1,004 ⋅ 10¹⁴
3. 6,100 ⋅ 10¹³
4. 5,232 ⋅ 10¹³
5. 2,616 ⋅ 10¹³

73. (Santa Casa) A figura indica a posição inicial da coreografia de três dançarinos, Ana (A), Bruna (B) e Caio (C), sendo ABC um triângulo equilátero inscrito em uma circunferência de centro O.

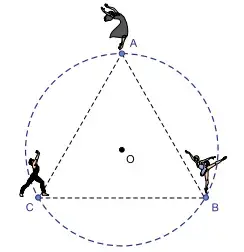
No próximo movimento da coreografia, Ana vai deslocar-se 30º sobre a circunferência, em sentido anti-horário; Bruna vai deslocar-se 60º sobre a circunferência, em sentido horário, e Caio vai deslocar-se 45º sobre a circunferência, em sentido anti-horário. Após essa movimentação dos três, a medida do menor ângulo interno do triângulo com vértices nas novas posições dos três dançarinos será de

1. 6,5º.
2. 7,5º.
3. 15º.
4. 22,5º.
5. 12º

74. (Santa Casa) Uma urna contém cartões com as 26 letras do alfabeto. Retirando-se aleatoriamente 4 cartões de uma única vez dessa urna, a probabilidade de que com eles seja possível, em alguma ordem das letras, formar a palavra VIDA é igual a

1. 2/7475
2. 1/7475
3. 3/1495
4. 1/14950
5. 6/7475

75. (Santa Casa) O gráfico indica a representação da elipse de equação $\frac{x^2}{16}+\frac{y^2}{25}$ = 81 e de duas circunferências, de centros com coordenadas (-20,0) e (20,0), que tangenciam a elipse nos pontos em que ela intersecta o eixo das abscissas. As retas r e s passam pela origem do sistema cartesiano de eixos ortogonais e tangenciam as circunferências nos pontos A, C, B e D, como mostra a figura.

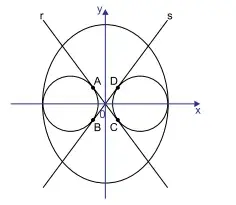
Na situação descrita, a área do retângulo ABCD, em unidades de área do plano cartesiano, é igual a

1. $\frac{6912}{25}$
2. $\frac{3456}{25}$
3. $\frac{1728}{25}$
4. $\frac{13829}{50}$
5. $\frac{13949}{50}$

76. (Santa Casa) A figura indica triângulos retângulos CBA e MBD. Os pontos A, M e B são colineares, assim como também são colineares os pontos C, B e D. Os ângulos CÂB e MDB e são congruentes. Sabe-se ainda que AM = BM = 1 cm e que CB + BD = $\frac{5\sqrt{3}}{3}$ cm, com CB < BD.

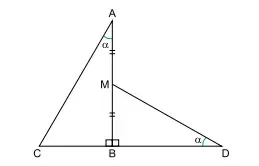
Nas condições descritas, a mediana do triângulo ABC é igual a

1. $\sqrt{\frac{7}{3}}$
2. $\sqrt{\frac{8}{3}}$
3. $\sqrt{\frac{6}{2}}$
4. $\sqrt{\frac{5}{2}}$
5. $\frac{16\sqrt{3}}{25}$

Resolução OBJETIVO: Observação: Utilizando-se a inversa da matriz M fornecida pelo examinador, e é isso que o aluno PODERIA e DEVERIA fazer, conclui-se que x + y + z = 50/59 que é o resultado CORRETO, de acordo com o gabarito oficial. A matriz inversa fornecida, porém, NÃO ESTÁ correta. O elemento da segunda linha e segunda coluna É 33/118 e NÃO 33/59.

77. (Santa Casa) Observe a matriz quadrada M e sua inversa M^–1

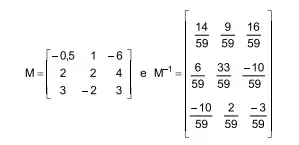
A soma dos valores de x, y e z que resolvem o sistema linear

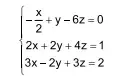
é igual a

1. $\frac{49}{59}$
2. $\frac{48}{59}$
3. $\frac{50}{59}$
4. $\frac{52}{59}$
5. $\frac{51}{59}$

78. (Santa Casa) Em uma reta são marcados os pontos distintos P, Q, R e S, nessa ordem, tal que PQ = 1 e QS = 2. Se as medidas PQ, QR e RS serão utilizadas como lados de um triângulo, então todos os valores possíveis para QR estão no intervalo real

1. $]\frac{3}{2},2[$
2. $]\frac{1}{2},\frac{3}{2}[$
3. $]\frac{3}{5}·\; <!--\; middle\; dot\; -->\frac{6}{5}[$
4. $]1,\frac{3}{2}[$
5. $]\frac{7}{4},2[$

79. (Santa Casa) O decaimento radioativo de uma substância se dá de acordo com a fórmula r(t) = C ⋅ 3^–6t, com C sendo uma constante diferente de zero e r(t) a quantidade de radioatividade presente na substância após t segundos desde o início do decaimento. O valor de t, em segundos, para que a substância fique com a terça parte da radioatividade que tinha incialmente é igual a

1. $\frac{1}{4}$
2. $\frac{1}{5}$
3. $\frac{1}{3}$
4. $\frac{1}{6}$
5. $\frac{2}{5}$

80. (Santa Casa) A figura indica o gráfico da função f: ℝ→ℝ, , definida por f(x) = x ⋅ sen(x), e a abscissa de dois dos seus pontos, cujas ordenadas são P e Q.

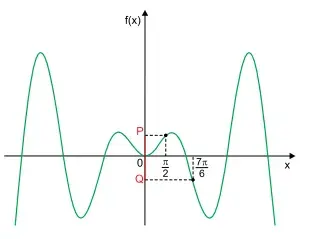
Nas condições descritas, P+ Q é igual a

1. - $\frac{\mathrm{\pi }}{12}$
2. $\frac{\mathrm{\pi }}{18}$
3. - $\frac{\mathrm{\pi }}{3}$
4. - $\frac{\mathrm{\pi }}{6}$
5. - $\frac{\mathrm{\pi }}{18}$