Geografia Plana III

01. (AFA) Considere no plano cartesiano as retas r e s dadas pelas equações:

r: 3x + 3py + p = 0

s: px + 9y – 3 = 0

, onde p ∈ IR

Baseado nessas informações, marque a alternativa INCORRETA

1. r e s são retas concorrentes se |p| ≠ 3
2. Existe um valor de p para o qual r é equação do eixo das ordenadas e s é perpendicular a r.
3. r e s são paralelas distintas para dois valores reais de p.
4. r e s são retas coincidentes para algum valor de p.

02. (EEAR) Se o perímetro do triângulo abaixo é maior que 18, o valor de x é

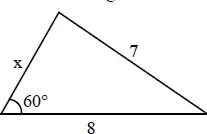
1. 4
2. 5
3. 6
4. 7

03. (EEAR) Seja ABCD um paralelogramo com AB // CD e BC // AD . Se a interseção de AC e BD é o ponto O, sempre é possível garantir que

1. AO = BO
2. AB = CB
3. DO = BO
4. AD = CD

04. (CN) Uma placa será confeccionada de modo que o emblema da empresa seja feito de um metal que custa R$ 5,00 o centímetro quadrado. O emblema consiste em três figuras planas semelhantes que lembram três árvores. Para as bases dessas "árvores", constroem-se segmentos de reta proporcionais a 3, 4 e 5.

Se o custo da maior árvore do emblema ficou em R$ 800,00, qual o valor, em reais, de todo o emblema?

1. 1600
2. 1500
3. 1200
4. 1120
5. 1020

05. (EEAR) Duas crianças resolvem apostar corrida em uma praça cuja geometria é representada na figura abaixo. Sabendo que a criança I percorre o caminho ABC e que a criança II percorre o caminho AC, podemos afirmar que a diferença entre a distância percorrida pela criança I e a criança II, vale, em metros:

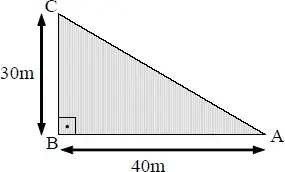
1. 20
2. 30
3. 40
4. 50

06. (CN) Observe a figura a seguir.

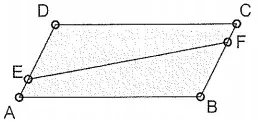
ABCD é um paralelogramo. E e F estão sobre os lados desse paralelogramo de tal forma que AE = CF = x < AD.

Sendo assim, baseado na figura acima, assinale a opção correta.

1. Qualquer reta que intersecte dois lados de um paralelogramo o divide em dois polígonos de mesma área.
2. Qualquer reta que intersecte dois lados de um paralelogramo o divide em dois polígonos de mesmo perímetro.
3. A área de um trapézio é o produto de sua base média pela sua altura.
4. O dobro da soma dos quadrados das medidas dos lados paralelos de um trapézio é igual à soma dos quadrados das medidas de suas diagonais.
5. Para todo x, o segmento de reta EF é metade do segmento de reta AB.

07. (CN) Um triângulo isósceles ABC tem base BC = 16 cm e lados congruentes AB = AC = 17 cm.

O raio do círculo inscrito ao triângulo ABC em cm é igual a:

1. 32/15
2. 24/5
3. 35/8
4. 28/5
5. 17/4

08. (EEAR) O triângulo determinado pelos pontos A(-1, -3), B(2, 1) e C(4, 3) tem área igual a

1. 1
2. 2
3. 3
4. 6

09. (ESA) Os ângulos internos de um quadrilátero são inversamente proporcionais aos números 2, 3, 4 e 5.

O maior ângulo interno desse quadrilátero mede, aproximadamente:

1. 210°
2. 90°
3. 230°
4. 100°
5. 140°

10. (CN) Para capinar um terreno circular plano, de raio 7m, uma máquina gasta 5 horas.

Quantas horas gastará essa máquina para capinar um terreno em iguais condições com 14m de raio?

1. 10
2. 15
3. 20
4. 25
5. 30

11. (ESA) Uma caixa d’água na forma de um paralelepípedo reto de base quadrada, cuja altura é metade do lado da base e tem medida k, está com 80% de sua capacidade máxima ocupada.

Sabendo-se que há uma torneira de vazão 50 L/min enchendo essa caixa d’água e que após 2h ela estará completamente cheia, qual o volume de uma caixa d’água cúbica de aresta k?

1. 7.500 mL
2. 6.000 mL
3. 7.500 dm³
4. 6.000 cm³
5. 5.000 mL

12. (CN) Qual a medida da maior altura de um triângulo de lados 3, 4, 5?

1. 12/5
2. 3
3. 4
4. 5
5. 20/3

13. (EPCAR) Um escritório de engenharia foi contratado para desenhar um projeto de construção de uma praça.

Para a execução do projeto, deverão ser atendidas as seguintes condições:

• a praça será em forma de um triângulo escaleno;

• as medidas dos lados da praça são números inteiros;

• a medida do maior lado é o dobro da medida do menor lado;

• o perímetro da praça é 120 metros.

O número de projetos que poderão ser executados, atendendo às condições acima, é x.

O número x é

1. múltiplo de 7
2. primo maior que 3
3. divisor de 27
4. quadrado perfeito menor que 20

14. (CN) Num semicírculo S, inscreve-se um triângulo retângulo ABC. A maior circunferência possível que se pode construir externamente ao triângulo ABC e internamente ao S, mas tangente a um dos catetos de ABC e ao S, tem raio 2. Sabe-se ainda que o menor cateto de ABC mede 2.

Qual a área do semicírculo?

1. 10π
2. 12,5π
3. 15π
4. 17,5π
5. 20π

15. (EN) Rola-se, sem deslizar, uma roda de 1 metro de diâmetro, por um percurso reto de 30 centímetros, em uma superfície plana.

O ângulo central de giro da roda, em radianos, é

1. 0,1
2. 0,2
3. 0,3
4. 0,6
5. 0,8

16. (EPCAR) Considere o octógono regular ABCDEFG inscrito numa circunferência λ de raio R

Se esse mesmo octógono circunscreve uma circunferência α de raio r, então a razão entre os quadrados dos comprimentos das circunferências λ e α é, nessa ordem, igual a

1. (2 + √2)
2. 2 (2 + √2)
3. 2(2 - √2)
4. 2 - √2

17. (EPCAR) Uma escola tem 10 salas de aula. Em todas elas cada uma das quatro paredes mede 500 cm de comprimento e 0,3 dam de altura. Deseja-se pintar as paredes dessas salas com tinta branca e para isso foram comprados galões de 36 dl por R$ 54,00 cada um. O pintor calculou que, para pintar cada 12m2 de parede, gastará 3 l dessa tinta e um tempo de 24 minutos. Sabe-se que ele cobra R$ 20,00 por hora trabalhada.

Com base nessas informações, é correto afirmar que

1. serão necessários mais de 41galões de 3,6 l para essa pintura.
2. para pintar todas as paredes serão gastos menos de R$ 2 000,00 com tinta.
3. serão necessárias apenas 18 horas de trabalho para pintar as 10 salas de aula.
4. o pintor receberá, em reais, ao final da pintura, o valor equivalente ao de 8 galões de tinta.

18. (EsPCEx) Considere um plano α e os pontos A, B, C e D tais que

· O segmento AB tem 6 cm de comprimento e está contido em α.

· O segmento BC tem 24 cm de comprimento, está contido em α e é perpendicular a AB.

· O segmento AD tem 8 cm de comprimento e é perpendicular a α.

Nessas condições, a medida do segmento CD é

1. 26 cm
2. 28 cm
3. 30 cm
4. 32 cm
5. 34 cm

19. (EPCAR) Samuel possui 12 palitos iguais e resolveu formar um único triângulo por vez, usando os 12 palitos sem parti-los. Ele verificou que é possível formar x triângulos retângulos, y triângulos isósceles, z triângulos equiláteros e w triângulos escalenos.

A soma x + y + z + w é igual a

1. 7
2. 6
3. 5
4. 4

20. (ESA) Os pontos M (– 3, 1) e P (1, – 1) são equidistantes do ponto S (2, b).

Desta forma, pode-se afirmar que b é um número

1. primo.
2. múltiplo de 3.
3. divisor de 10.
4. irracional.
5. maior que 7.