Geometria Analítica
Lista de 11 exercícios de Matemática com gabarito sobre o tema Geometria Analítica com questões da Fuvest.
01. (Fuvest 2017) Duas circunferências com raios 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x1, y1) e (x2, y2).
O valor de (x1 + y1)² + (x2 + y2)² é igual a
02. (Fuvest 2016) No plano cartesiano, um círculo de centro P = (a,b) tangencia as retas de equações y = x e x = 0. Se P pertence à parábola de equação y = x2 e a > 0, a ordenada b do ponto P é igual
- 2 + 2√2
- 3 + 2√2
- 4 + 2√2
- 5 + 2√2
- 6 + 2√2
03. (Fuvest 2015) A equação x² + 2x + y² + my = n, em que m e n são constantes, representa uma circunferncia no plano cartesiano.
Sabe se que a reta y = -x +1 contém o centro da circunferência e a intersecta no ponto (-3,4). Os valores de m e n são, respectivamente,
- -4 e 3
- 4 e 5
- -4 e 2
- -2 e 4
- 2 e 3
04. (Fuvest 2014) Considere o triângulo no plano cartesiano com vértices A = (0,0), B = (3,4) e C = (8,0). O retângulo MNPQ tem os vértices M e N sobre o eixo das abscissas, o vértice Q sobre o lado AB e o vértice P sobre o lado BC.
05. (Fuvest 2013) São dados, no plano cartesiano, o ponto P de coordenadas (3,6) e a circunferência de equação C = (x - 1)² + (y - 2)². Uma reta t passa por P e é tangente a C em um ponto Q.
Então a distância de P a Q é
- √15
- √17
- √18
- √19
- √20
06. (Fuvest 2012) No plano cartesiano Oxy, a circunferência C é tangente ao eixo Ox no ponto de abscissa 5 e contém o ponto (1,2).
Nessas condições, o raio C vale
- √5
- 2√5
- 5
- 3√5
- 10
07. (Fuvest 2011) No plano cartesiano, os pontos (0, 3) e (–1, 0) pertencem à circunferência C. Uma outra circunferência, de centro em , é tangente a C no ponto(0, 3). Então, o raio de C vale
08. (Fuvest) No plano cartesiano Oxy, a reta de equação x + y = 2 é tangente à circunferência C no ponto (0, 2). Além disso, o ponto (1, 0) pertence a C. Então, o raio de C é igual a
09. (Fuvest 2009) Considere, no plano cartesiano Oxy, a circunferência C de equação (x-2)² + (y-2)²= 4 e sejam P e Q os pontos nos quais C Tangencia os Eixos Ox e Oy respectivamente.
Seja PQR o triângulo isósceles inscrito em C, de base PQ , e como maior perímetro possível
Então, a área de PQR é igual a.
- 2√2 - 2
- 2√2 - 1
- 2√2
- 2√2 + 2
- 2√2 + 4
10. (Fuvest 2008) A circunferência dada pela equação x² + y² – 4x – 4y + 4 = 0 é tangente aos eixos coordenados x e y nos pontos A e B, conforme a figura.
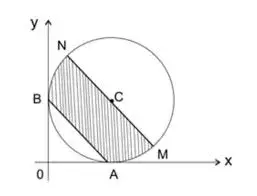
O segmento MN é paralelo ao segmento AB e contém o centro C da circunferência.
É correto afirmar que a área da região hachurada vale
- π - 2
- π + 6
- π + 4
- π + 6
- π + 8
11. (Fuvest 2005) A soma das distâncias de um ponto interior de um triângulo eqüilátero aos seus lados é 9. Assim, a medida do lado do triângulo é
- 5√3
- 6√3
- 7√3
- 8√3
- 9√3